suivant: Symbolic constants : e monter: Symbolic algebra and Mathematics précédent: Table des matières Table des matières Index

The CAS functions

Sous-sections

Symbolic constants : e pi infinity i
Booleans
- The values of a boolean : true false
- Tests : ==, !=, >, >=, <, =<
- Boolean operators : or xor and not
- Transform a boolean expression as a list : exp2list
- Evaluate booleans : evalb
Operators bit to bit
- Operators bitor, bitxor, bitand
- Hamming distance bit to bit : hamdist
Strings
- Character and string : "
- First character, middle and end of a string : head mid tail
- Concatenation of a sequence of words : cumSum
- ASCII code of a character : ord
- ASCII code of a string : asc
- String defined by the ASCII codes of its characters : char
- Find a character in a string : inString
- Concat objects into a string : cat
- Add an object to a string : +
- Transform an integer into a string : cat +
- Transform a string into a number : expr
Write an integer in a b basis: convert
Integers (and Gaussian Integers)
- The factorial : factorial
- GCD : gcd igcd
- GCD : Gcd
- GCD of a list of integers : lgcd
- The least common multiple : lcm
- Decomposition into prime factors : ifactor
- List of prime factors : ifactors
- Matrix of factors : maple_ifactors
- The divisors of a number : idivis divisors
- The integer Euclidean quotient : iquo intDiv
- The integer Euclidean remainder : irem remain smod mods mod %
- Euclidean quotient and euclidean remainder of two integers : iquorem
- Test of evenness : even
- Test of oddness : odd
- Test of pseudo-primality : is_pseudoprime
- Test of primality : is_prime isprime isPrime
- The smallest pseudo-prime greater than n : nextprime
- The greatest pseudo-prime less than n : prevprime
- The n-th prime number : ithprime
- Bézout's Identity : iegcd igcdex
- Solving au+bv=c in $\mathbb {Z}$ : iabcuv
- Chinese remainders : ichinrem, ichrem
- Chinese remainders for lists of integers : chrem
- Solving a² + b² = p in $\mathbb {Z}$ : pa2b2
- The Euler indicatrix : euler phi
- Legendre symbol : legendre_symbol
- Jacobi symbol : jacobi_symbol
Combinatory analysis
- Factorial : factorial !
- Binomial coefficients : binomial comb nCr
- Arrangements : perm nPr
- Random integers : rand
Rationals
- Transform a floating point number into a rational : exact float2rational
- Integer and fractional part : propfrac propFrac
- Numerator of a fraction after simplification : numer
  getNum
- Denominator of a fraction after simplification : denom getDenom
- Numerator and denominator of a fraction : f2nd fxnd
- Simplification of a pair of integers : simp2
- Continued fraction representation of a real : dfc
- Transform a continued fraction representation into a real : dfc2f
- The n-th Bernoulli number : bernoulli
- Access to PARI/GP commands: pari
Real numbers
- Eval a real at a given precision : evalf and Digits, DIGITS)
- Usual infixed functions on reals : +,-,*,/,^
- Usual prefixed functions on reals : rdiv
- n-th root : root
- Error function : erf
- Complementary error function: erfc
- The 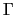$\Gamma$ function : Gamma
- The 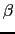$\beta$ function : Beta
- Derivatives of the DiGamma fonction : Psi
- The 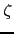$\zeta$ function : Zeta
- Airy functions : Airy_Ai and Airy_Bi
Permutations
- Random permutation : randperm
- Decomposition as a product of disjoint cycles :
  permu2cycles
- Product of disjoint cycles to permutation: cycles2permu
- Transform a cycle into permutation : cycle2perm
- Transform a permutation into a matrix : permu2mat
- Checking for a permutation : is_permu
- Checking for a cycle : is_cycle
- Product of two permutations : p1op2
- Composition of a cycle and a permutation : c1op2
- Composition of a permutation and a cycle : p1oc2
- Product of two cycles : c1oc2
- Signature of a permutation : signature
- Inverse of a permutation : perminv
- Inverse of a cycle : cycleinv
- Order of a permutation : permuorder
- Group generated by two permutations : groupermu
Complex numbers
- Usual complex functions : +,-,*,/,^
- Real part of a complex number : re real
- Imaginary part of a complex number : im imag
- Write a complex as re(z)+i*im(z) : evalc
- Modulus of a complex number : abs
- Argument of a complex number : arg
- The normalized complex number : normalize unitV
- Conjuguate of a complex number : conj
- Multiplication by the complex conjugate :
  mult_c_conjugate
- Barycenter of complex numbers : barycentre
Algebraic expressions
- Evaluate an expression : eval
- Evaluate algebraic expressions : evala
- Prevent evaluation : quote hold '
- Force evaluation : unquote
- Distributivity : expand fdistrib
- Canonical form : canonical_form
- Multiplication by the conjugate quantity :
  mult_conjugate
- Separation of variables : split
- Factorisation : factor
- Complex factorisation : cFactor
- Zeros of an expression : zeros
- Complex zeros of an expression : cZeros
- Normal form : normal
- Simplify : simplify
- Normal form for rational fractions : ratnormal
- Substitue a variable by a value : subst
- Substitue a variable by a value (Maple and Mupad compatibility) : subs
- Evaluate a primitive at boundaries: preval
- Sub-expression of an expression : part
Values of u_n
- Array of values of a sequence : tablefunc
- Table of values and graph of a recurrent sequence : tableseq and plotseq
Operators or infixed functions
- Usual operators :+, -, *, /, ^
- Xcas operators
- Define an operator: user_operator
Functions and expressions with symbolic variables
- Difference between function and expression
- Transform an expression into a fonction : unapply
- Top and leaves of an expression : sommet feuille op
Functions
- Context-dependant functions.
- Usual functions
- Defining algebraic functions
- Composition of two functions: @
- Repeted function composition: @@
- Define a fonction with the history : as_function_of
Derivation and applications.
- Functional derivative : function_diff
- Length of an arc : arcLen
- Maximum and minimum of an expression: fMax fMin
- Table of values and graph : tablefunc and plotfunc
- Derivative and partial derivative
  - Derivative and first order partial derivative : diff derive deriver
  - Derivative and n-th order partial derivative : diff derive deriver
Integration
- Antiderivative and definite integral : integrate int Int
- Discrete summation: sum
- Riemann sum : sum_riemann
- Integration by parts : ibpdv et ibpu
  - ibpdv
  - ibpu
- Change of variables : subst
Limits
- Limites : limit
- Integral and limit
Rewriting transcendental and trigonometric expressions
- Expand a transcendental and trigonometric expression : texpand tExpand
- Combine terms of same type : combine
Trigonometry
- Trigonometric functions
- Expand a trigonometric expression : trigexpand
- Linearize a trigonometric expression : tlin
- Put together sine and cosine of the same angle : tcollect tCollect
- Simplify : simplify
- Transform arccos into arcsin : acos2asin
- Transform arccos into arctan : acos2atan
- Transform arcsin into arccos : asin2acos
- Transform arcsin into arctan : asin2atan
- Transform arctan into arcsin : atan2asin
- Transform arctan into arccos : atan2acos
- Transform complex exponentials into sin and cos : sincos exp2trig
- Transform tan(x) into sin(x)/cos(x) : tan2sincos
- Rewrite tan(x) with sin(2x) and cos(2x) : tan2sincos2
- Rewrite tan(x) with cos(2x) and sin(2x) : tan2cossin2
- Rewrite sin, cos, tan in terms of tan(x/2) : halftan
- Rewrite trigonometric functions as function of tan(x/2) and hyperbolic functions as function of exp(x):
  halftan_hyp2exp
- Transform inverse trigonometric functions into logarithms : atrig2ln
- Transform trigonometric functions into complex exponentials : trig2exp
- Simplify and express preferentially with sine : trigsin
- Simplify and express preferentially with cosine : trigcos
- Simplify and express preferentially with tangents : trigtan
- Rewrite an expression with different options : convert convertir
Fourier transformation
- Fourier coefficients : fourier_an and fourier_bn or fourier_cn
- Discrete Fourier Transform
  - The properties of the Discrete Fourier Transform
  - Applications
- Fast Fourier Transform : fft
- Inverse Fast Fourier Transform : ifft
- An exercice with fft
Exponentials and Logarithms
- Rewrite hyperbolic functions as exponentials : hyp2exp
- Expand exponentials : expexpand
- Expand logarithms : lnexpand
- Linearize exponentials : lin
- Collect logarithms : lncollect
- Expand powers : powexpand
- Rewrite a power as an exponential : pow2exp
- Rewrite exp(n*ln(x)) as a power : exp2pow
- Simplify complex exponentials : tsimplify
Polynomials
- Convert to a symbolic polynomial : r2e poly2symb
- Convert from a symbolic polynomial : e2r symb2poly
- Coefficients of a polynomial: coeff coeffs
- Polynomial degree : degree
- Polynomial valuation : valuation ldegree
- Leading coefficient of a polynomial : lcoeff
- Trailing coefficient degree of a polynomial : tcoeff
- Evaluation of a polynomial : peval polyEval
- Factorize xⁿ in a polynomial : factor_xn
- GCD of the coefficients of a polynomial : content
- Primitive part of a polynomial : primpart
- Factorization : collect
- Factorization : factor factoriser
- Square-free factorization : sqrfree
- List of factors : factors
- Evaluate a polynomial : horner
- Rewrite in terms of the powers of (x-a) : ptayl
- Compute with the exact root of a polynomial : rootof
- Exact roots of a polynomial : roots
- Coefficients of a polynomial defined by its roots : pcoeff pcoef
- Truncate of order n : truncate
- Convert a series expansion into a polynomial : convert convertir
- Random polynomial : randpoly randPoly
- Change the order of variables : reorder
- Random list : ranm
- Lagrange's polynomial : lagrange interp
- Natural splines: spline
  - Definition
  - Theorem
  - Interpolation with spline functions
Arithmetic and polynomials
- The divisors of a polynomial : divis
- Euclidean quotient : quo
- Euclidean quotient : Quo
- Euclidean remainder : rem
- Euclidien remainder: Rem
- Quotient and remainder : quorem divide
- GCD of two polynomials with Euclide algorithm: gcd
- GCD of two polynomials with Euclide algorithm : Gcd
- Choosing the GCD algorithm of two polynomials : ezgcd heugcd modgcd psrgcd
- LCM of two polynomials : lcm
- Bézout's Identity : egcd gcdex
- Solving au+bv=c over polynomials: abcuv
- Chinese remainders : chinrem
- Cyclotomic polynomial : cyclotomic
- Sturm sequences and number of sign changes of P on ]a; b] : sturm
- Number of zeros in [a, b[ : sturmab
- Sturm sequences : sturmseq
- Sylvester matrix of two polynomials : sylvester
- Resultant of two polynomials : resultant
Orthogonal polynomials
- Legendre polynomials: legendre
- Hermite polynomial : hermite
- Laguerre polynomials: laguerre
- Tchebychev polynomials of first kind: tchebyshev1
- Tchebychev polynomial of second kind: tchebyshev2
Gröbner basis and Gröbner reduction
- Gröbner basis : gbasis
- Gröbner reduction : greduce
- Build a polynomial from it's evaluation : genpoly
Rational fractions
- Numerator : getNum
- Numerator after simplification : numer
- Denominator : getDenom
- Denominator after simplification : denom
- Numerator and denominator : f2nd fxnd
- Simplify : simp2
- Common denominator : comDenom
- Integer and fractional part : propfrac
- Partial fraction expansion : partfrac
Exact roots of a polynomial
- Exact bounds for complex roots of a polynomial :
  complexroot
- Exact bounds for real roots of a polynomial : realroot
- Exact values of rational roots of a polynomial :
  rationalroot
- Exact values of the complex rational roots of a polynomial : crationalroot
Exact roots and poles
- Roots and poles of a rational function : froot
- Rational function given by roots and poles : fcoeff
Computing in $\mathbb {Z}$ /p $\mathbb {Z}$ or in $\mathbb {Z}$ /p $\mathbb {Z}$ [x]
- Expand and reduce : normal
- Addition in $\mathbb {Z}$ /p $\mathbb {Z}$ or in $\mathbb {Z}$ /p $\mathbb {Z}$ [x] : +
- Substraction in $\mathbb {Z}$ /p $\mathbb {Z}$ or in $\mathbb {Z}$ /p $\mathbb {Z}$ [x] : -
- Multiplication in $\mathbb {Z}$ /p $\mathbb {Z}$ or in $\mathbb {Z}$ /p $\mathbb {Z}$ [x] : *
- Euclidian quotient : quo
- Euclidian remainder : rem
- Euclidian quotient and euclidian remainder : quorem
- Division in $\mathbb {Z}$ /p $\mathbb {Z}$ or in $\mathbb {Z}$ /p $\mathbb {Z}$ [x] : /
- Power in $\mathbb {Z}$ /p $\mathbb {Z}$ and in $\mathbb {Z}$ /p $\mathbb {Z}$ [x] : ^
- Compute aⁿ mod p : powmod powermod
- Inverse in $\mathbb {Z}$ /p $\mathbb {Z}$ : inv inverse or /
- Rebuild a fraction from it's value modulo p : fracmod
- GCD in $\mathbb {Z}$ /p $\mathbb {Z}$ [x] : gcd
- Factorization over $\mathbb {Z}$ /p $\mathbb {Z}$ [x] : factor factoriser
- Determinant of a matrix in $\mathbb {Z}$ /p $\mathbb {Z}$ : det
- Inverse of a matrix with coefficients in $\mathbb {Z}$ /p $\mathbb {Z}$ : inv inverse
- Row reduction to echelon form in $\mathbb {Z}$ /p $\mathbb {Z}$ : rref
- Construction of a Galois field : GF
- Factorize a polynomial with coefficients in a Galois field : factor
Compute in $\mathbb {Z}$ /p $\mathbb {Z}$ [x] using Maple syntax
- Euclidean quotient : Quo
- Euclidien remainder: Rem
- GCD in $\mathbb {Z}$ /p $\mathbb {Z}$ [x] : Gcd
- Factorization in $\mathbb {Z}$ /p $\mathbb {Z}$ [x] : Factor
- Determinant of a matrix with coefficients in $\mathbb {Z}$ /p $\mathbb {Z}$ : Det
- Inverse of a matrix in $\mathbb {Z}$ /p $\mathbb {Z}$ : Inverse
- Row reduction to echelon form in $\mathbb {Z}$ /p $\mathbb {Z}$ : Rref
Taylor and asymptotic expansions
- Division by increasing power order : divpc
- Taylor expansion : taylor
- Series expansion : series
- Résidu d'une expression en un point : residue
- Padé expansion: pade
Intervals
- Definition of an interval : a1..a2
- Boundaries of an interval : left right
- Center of an interval : interval2center
- Intervals defined by their center : center2interval
Sequences
- Definition : seq[] ()
- Concat two sequences : ,
- Get an element of a sequence : []
- Sub-sequence of a sequence : []
- Make a sequence or a list : seq $
- Transform a sequence into a list : [] nop
- The + operator applied on sequences
Sets
- Definition : set[]
- Union of two sets or of two lists : union
- Intersection of two sets or of two lists : intersect
- Difference of two sets or of two lists : minus
Lists and vectors
- Definition
- Get an element or a sub-list of a list : at []
  - Get an element
  - Extract a sub-list
- Extract a sub-list : mid
- Get the first element of a list : head
- Remove an element in a list : suppress
- Remove the first element : tail
- Reverse order in a list : revlist
- Reverse a list starting from its n-th element : rotate
- Permuted list from its n-th element : shift
- Modify an element in a list : subsop
- Transform a list into a sequence : op makesuite
- Transform a sequence into a list : makevector []
- Length of a list : size nops length
- Sizes of a list of lists : sizes
- Concatenate two lists or a list and an element : concat augment
- Append an element at the end of a list : append
- Prepend an element at the begining of a list : prepend
- Sort : sort
- Sort a list by increasing order : SortA
- Sort a list by decreasing order : SortD
- Select the elements of a list : select
- Remove elements of a list : remove
- Test if a value is in a list : member
- Test if a value is in a list : contains
- Sum of list (or matrix) elements transformed by a function : count
- Number of elements equal to a given value : count_eq
- Number of elements smaller than a given value : count_inf
- Number of elements greater than a given value : count_sup
- Sum of elements of a list : sum add
- Cumulated sum of the elements of a list : cumSum
- Product : product mul
  - Product of values of an expression : product
  - Product of elements of a list : product
- Apply a function of one variable to the elements of a list : map apply of
- Apply a bivariate function to the elements of two lists : zip
- Make a list with zeros : newList
- Make a list with a function : makelist
- Make a random vector or list : randvector
- List of differences of consecutive terms : deltalist
- Make a matrix with a list : list2mat
- Make a list with a matrix : mat2list
Functions for vectors
- Norms of a vector : maxnorm l1norm l2norm norm
- Normalize a vector : normalize unitV
- Term by term sum of two lists : + .+
- Term by term difference of two lists : - .-
- Term by term product of two lists : .*
- Term by term quotient of two lists : ./
- Scalar product : scalar_product * dotprod dot dotP scalar_Product
- Cross product : cross crossP crossproduct
Statistic functions : mean,variance,stddev, stddevp,median,quantile,quartiles,boxwhisker
Table with string as index : table
Usual matrix
- Identity matrix : idn identity
- Zero matrix : newMat matrix
- Random matrix : ranm randMat randmatrix
- Diagonal of a matrix or matrix of a diagonal : BlockDiagonal diag
- Jordan bloc : JordanBlock
- Hilbert matrix : hilbert
- Vandermonde matrix : vandermonde
Arithmetic and matrix
- Evaluate a matrix : evalm
- Addition and substraction of two matrices : + - .+ .-
- Multiplication of two matrices : * &*
- Addition of elements of a column of a matrix : sum
- Cumulated sum of elements of each column of a matrix : cumSum
- Multiplication of elements of each column of a matrix : product
- Power of a matrix : ^ &^
- Hadamard product : hadamard product
- Hadamard product (infixed version): .*
- Hadamard division (infixed version): ./
- Hadamard power (infixed version): .^
- Extracting element(s) of a matrix : [] at
- Modify an element or a row of a matrix : subsop
- Extract rows or columns of a matrix (Maple compatibility) : row col
- Remove rows or columns of a matrix : delrows delcols
- Extract a sub-matrix of a matrix (TI compatibility) : subMat
- Add a row to another row : rowAdd
- Multiply a row by an expression : mRow
- Add k times a row to an another row : mRowAdd
- Exchange two rows : rowSwap
- Make a matrix with a list of matrix : blockmatrix
- Make a matrix from two matrices : semi_augment
- Make a matrix from two matrices : augment concat
- Build a matrix with a function : makemat
- Define a matrix : matrix
- Append a column to a matrix : border
- Count the elements of a matrix verifying a property : count
- Count the elements equal to a given value : count_eq
- Count the elements smaller than a given value : count_inf
- Count the elements greater than a given value : count_sup
- Statistics functions acting on column matrices : mean, stddev, variance, median, quantile, quartiles, boxwhisker
- Dimension of a matrix : dim
- Number of rows : rowdim rowDim nrows
- Number of columns : coldim colDim ncols
Linear algebra
- Transpose of a matrix : tran transpose
- Inverse of a matrix : inv /
- Trace of a matrix : trace
- Determinant of a matrix : det
- Determinant of a sparse matrix : det_minor
- Rank of a matrix : rank
- Transconjugate of a matrix : trn
- Equivalent matrix : changebase
- Basis of a linear subspace : basis
- Basis of the intersection of two subspaces : ibasis
- Image of a linear application : image
- Kernel of a linear application : kernel nullspace ker
- Kernel of a linear application : Nullspace
- Subspace generated by the columns of a matrix : colspace
- Subspace generated by the rows of a matrix : rowspace
Linear Programmation
- Simplex algorithm: simplex_reduce
Different matrix norm
- l² matrix norm : nomm l2norm
- l 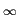matrix norm : maxnorm
- Matrix row norm : rownorm rowNorm
- Matrix column norm : colnorm colNorm
Matrix reduction
- Eigenvalues : eigenvals
- Eigenvalues : egvl eigenvalues eigVl
- Eigenvectors : egv eigenvectors eigenvects eigVc
- Rational Jordan matrix : rat_jordan
- Jordan normal form : jordan
- Characteristic polynomial : charpoly
- Characteristic polynomial using Hessenberg algorithm :
  pcar_hessenberg
- Minimal polynomial : pmin
- Adjoint matrix : adjoint_matrix
- Companion matrix of a polynomial : companion
- Hessenberg matrix reduction : hessenberg
- Hermite normal form : ihermite
- Smith normal form : ismith
Isometries
- Recognize an isometry : isom
- Find the matrix of an isometry : mkisom
Matrix factorizations
- Cholesky decomposition : cholesky
- QR decomposition : qr
- QR decomposition (for TI compatibility) : QR
- LU decomposition : lu
- LU decomposition (for TI compatibility) : LU
- Singular value decomposition : svd
- Short basis of a lattice : lll
Quadratic forms
- Matrix of a quadratic form : q2a
- Transform a matrix into a quadratic form : a2q
- Reduction of a quadratic form : gauss
- Gramschmidt orthonormalization : gramschmidt
- Graph of a conic : conique
- Conic reduction : conique_reduite
- Graph of a quadric : quadrique
- Quadric reduction : quadrique_reduite
Multivariate calculus
- Gradient : derive deriver diff grad
- Laplacian : laplacian
- Hessian matrix : hessian
- Divergence : divergence
- Rotationnal : curl
- Potential : potential
- Conservative flux field : vpotential
Equations
- Define an equation : equal
- Transform an equation into a difference : equal2diff
- Transform an equation into a list : equal2list
- The left member of an equation : left gauche lhs
- The right member of an equation : right droit rhs
- Solving equation(s): solve
- Equation solving in 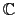$\mathbb {C}$ : cSolve
Linear systems
- Matrix of a system : syst2mat
- Gauss reduction of a matrix : ref
- Gauss-Jordan reduction: rref gaussjord
- Solving A*X=B : simult
- Step by step Gauss-Jordan reduction of a matrix : pivot
- Linear system solving: linsolve
- Finding linear recurrences : reverse_rsolve
Differential equations
- Solving differential equations : desolve deSolve dsolve
- Laplace transform and inverse Laplace transform : laplace ilaplace
Other functions
- Replace small values by 0: epsilon2zero
- List of variables : lname indets
- List of variables and of expressions : lvar
- List of variables of an algebraic expressions: algvar
- Test if a variable is in an expression : has
- Numeric evaluation : evalf
- Rational approximation : float2rational exact

giac documentation written by Renée De Graeve and Bernard Parisse