




suivant: Composition of two functions:
monter: Defining algebraic functions
précédent: Defining a function from
Table des matières
Index
Suppose that the function
f : (x, y) 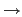 f (x, y) is defined,
and we want to define a family of functions g(t) such
that
g(t)(y) : = f (t, y) (i.e. t is viewed as a parameter).
Since the expression after -> (or :=)
is not evaluated, we should not define g(t) by g(t):=y->f(t,y),
we have to use the unapply command.
f (x, y) is defined,
and we want to define a family of functions g(t) such
that
g(t)(y) : = f (t, y) (i.e. t is viewed as a parameter).
Since the expression after -> (or :=)
is not evaluated, we should not define g(t) by g(t):=y->f(t,y),
we have to use the unapply command.
For example, assuming that
f : (x, y) 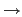 x sin(y) and
g(t) : y
x sin(y) and
g(t) : y 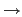 f (t, y), input :
f (t, y), input :
f(x,y):=x*sin(y);g(t):=unapply(f(t,y),y)
Output :
((x,y)->x*sin(y), (t)->unapply(f(t,y),y))
Input
g(2)
Output :
y->2 . sin(y)
Input
g(2)(1)
Output :
2 . sin(1)
Next example, suppose that the function
h : (x, y) 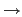 [x*cos(y), x*sin(y)] is defined, and
we want to define the family of functions k(t) having t as
parameter such that
k(t)(y) : = h(t, y).
To define the function h(x, y), input :
[x*cos(y), x*sin(y)] is defined, and
we want to define the family of functions k(t) having t as
parameter such that
k(t)(y) : = h(t, y).
To define the function h(x, y), input :
h(x,y):=(x*cos(y),x*sin(y))
To define properly the function k(t), input :
k(t):=unapply(h(x,t),x)
Output :
(t)->unapply(h(x,t),x)
Input
k(2)
Output :
(x)->(x*cos(2),x*sin(2))
Input
k(2)(1)
Output :
(2*cos(1),2*sin(1))





suivant: Composition of two functions:
monter: Defining algebraic functions
précédent: Defining a function from
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
![]() x sin(y) and
g(t) : y
x sin(y) and
g(t) : y ![]() f (t, y), input :
f (t, y), input :
![]() [x*cos(y), x*sin(y)] is defined, and
we want to define the family of functions k(t) having t as
parameter such that
k(t)(y) : = h(t, y).
To define the function h(x, y), input :
[x*cos(y), x*sin(y)] is defined, and
we want to define the family of functions k(t) having t as
parameter such that
k(t)(y) : = h(t, y).
To define the function h(x, y), input :