




suivant: Access to PARI/GP commands:
monter: Rationals
précédent: Transform a continued fraction
Table des matières
Index
The n-th Bernoulli number : bernoulli
bernoulli takes as argument an integer n.
bernoulli returns the n-th Bernoulli number B(n).
The Bernoulli numbers are defined by :
Bernoulli polynomials Bk are defined by :
B0 = 1,
Bk'(
x) =
kBk-1(
x),
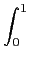 Bk
Bk(
x)
dx = 0
and the relation
B(n) = Bn(0) holds.
Input :
bernoulli(6)
Output :
1/42
giac documentation written by Renée De Graeve and Bernard Parisse
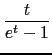 =
= 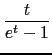 =
=