Euclidien remainder: Rem

Rem is the inert form of rem.
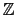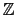Rem returns the euclidean remainder between two polynomials (decreasing power division) without evaluation. It is used when Xcas is in Maple mode to compute the euclidean remainder of the division of two polynomials with coefficients in $\mathbb {Z}$/p$\mathbb {Z}$ using Maple-like syntax.
In Xcas mode, input :

Rem(x^3-1,x^2-1)

Output :

rem(x^3-1,x^2-1)

In Maple mode, input :

Rem(x^3+3*x,2*x^2+6*x+5) mod 5

Output :

2*x

The division was done using modular arithmetic, unlike with

rem(x^3+3*x,2*x^2+6*x+5) mod 5

where the division is done in 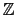$\mathbb {Z}$[X] and reduced after to:

12*x

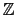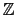If Xcas is not in Maple mode, polynomial division in $\mathbb {Z}$/p$\mathbb {Z}$[X] is done e.g. by :

rem((x^3+3*x)% 5,(2x^2+6x+5)%5)