




suivant: Combinatory analysis
monter: Integers (and Gaussian Integers)
précédent: Legendre symbol : legendre_symbol
Table des matières
Index
Jacobi symbol : jacobi_symbol
If n is not prime, the Jacobi symbol of a,
denoted as
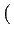
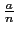
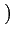 , is defined
from the Legendre symbol and from the
decomposition of n into prime factors.
Let
, is defined
from the Legendre symbol and from the
decomposition of n into prime factors.
Let
n =
p1
..
pk
where pj is prime and 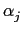 is an integer for j = 1..k.
The Jacobi symbol of a is defined by :
is an integer for j = 1..k.
The Jacobi symbol of a is defined by :
jacobi_symbol takes two arguments a and n, and it returns the Jacobi
symbol
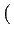
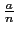
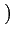 .
.
Input :
jacobi_symbol(25,12)
Output :
1
Input :
jacobi_symbol(35,12)
Output :
-1
Input :
jacobi_symbol(33,12)
Output :
0
giac documentation written by Renée De Graeve and Bernard Parisse