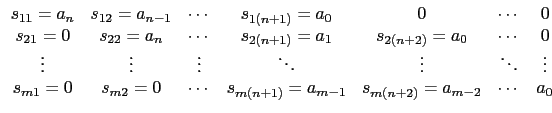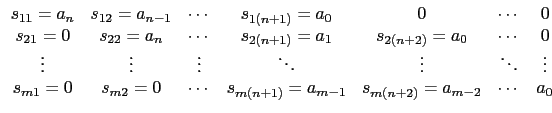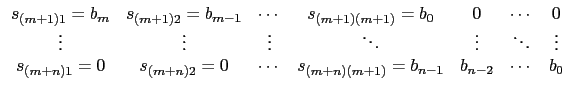Sylvester matrix of two polynomials : sylvester

sylvester takes two polynomials as arguments.
sylvester returns the Sylvester matrix S of these polynomials.
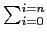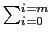If A(x) = $\sum_{{i=0}}^{{i=n}}$a_ixⁱ and B(x) = $\sum_{{i=0}}^{{i=m}}$b_ixⁱ are 2 polynomials, their Sylvester matrix S is a squared matrix of size m+n where m=degree(B(x)) and n=degree(A(x)). The m first lines are made with the A(x) coefficients, so that :

$$\left(\vphantom{\begin{array}{ccccccc} s_{11}=a_n & s_{12}=a_{n-1... ...ots & s_{m(n+1)}=a_{m-1} & s_{m(n+2)}=a_{m-2} & \cdots&a_0 \end{array}}\right.$$$$\begin{array}{ccccccc} s_{11}=a_n & s_{12}=a_{n-1}& \cdots & s_{1... ...}=0& \cdots & s_{m(n+1)}=a_{m-1} & s_{m(n+2)}=a_{m-2} & \cdots&a_0 \end{array}$$$$\left.\vphantom{\begin{array}{ccccccc} s_{11}=a_n & s_{12}=a_{n-1... ...ots & s_{m(n+1)}=a_{m-1} & s_{m(n+2)}=a_{m-2} & \cdots&a_0 \end{array}}\right)$$

and the n further lines are made with the B(x) coefficients, so that :

$$\left(\vphantom{\begin{array}{ccccccc} s_{(m+1)1}=b_m & s_{(m+1)2... ...}=0& \cdots & s_{(m+n)(m+1)}=b_{n-1} & b_{n-2} &\cdots&b_0 \end{array}}\right.$$$$\begin{array}{ccccccc} s_{(m+1)1}=b_m & s_{(m+1)2}=b_{m-1}& \cdot... ..._{(m+n)2}=0& \cdots & s_{(m+n)(m+1)}=b_{n-1} & b_{n-2} &\cdots&b_0 \end{array}$$$$\left.\vphantom{\begin{array}{ccccccc} s_{(m+1)1}=b_m & s_{(m+1)2... ...}=0& \cdots & s_{(m+n)(m+1)}=b_{n-1} & b_{n-2} &\cdots&b_0 \end{array}}\right)$$

Input :

sylvester(x^3-p*x+q,3*x^2-p,x)

Output :

[[1,0,-p,q,0],[0,1,0,-p,q],[3,0,-p,0,0], [0,3,0,-p,0],[0,0,3,0,-p]]

Input :

det([[1,0,-p,q,0],[0,1,0,-p,q],[3,0,-p,0,0], [0,3,0,-p,0],[0,0,3,0,-p]])

Output :

-4*p^3-27*q^2