




suivant: Arithmetic and polynomials
monter: Natural splines: spline
précédent: Theorem
Table des matières
Index
If we want to interpolate a function f on 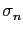 by a spline function
s of degree l, then s must verify
s(xk) = yk = f (xk) for all
0
by a spline function
s of degree l, then s must verify
s(xk) = yk = f (xk) for all
0 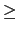 k
k 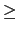 n. Hence there are n + 1 conditions, and l - 1 degrees of
liberty. We can therefore add l - 1 conditions, these conditions are on the
derivatives of s at a and b.
n. Hence there are n + 1 conditions, and l - 1 degrees of
liberty. We can therefore add l - 1 conditions, these conditions are on the
derivatives of s at a and b.
Hermite interpolation, natural interpolation and periodic interpolation
are three kinds of interpolation obtained by specifying three kinds
of constraints. The unicity of the
solution of the interpolation problem can be proved
for each kind of constraints.
If l is odd (l = 2m - 1), there are 2m - 2 degrees of
liberty. The constraints are defined by :
- Hermite interpolation
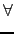
1
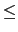 j
j 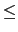 m
m - 1,
s(j)(
a) =
f(j)(
a),
s(j)(
b) =
f(j)(
b)
- Natural interpolation
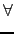 m
m 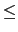 j
j 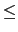
2
m - 2,
s(j)(
a) =
s(j)(
b) = 0
- periodic interpolation
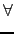
1
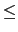 j
j 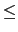
2
m - 2,
s(j)(
a) =
s(j)(
b)
If l is even (l = 2m), there are 2m - 1 degrees of
liberty. The constraints are defined by :
- Hermite interpolation
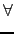
1
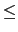 j
j 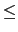 m
m - 1,
s(j)(
a) =
f(j)(
a),
s(j)(
b) =
f(j)(
b)
and
s(m)(a) = f(m)(a)
- Natural interpolation
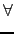 m
m 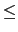 j
j 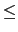
2
m - 2,
s(j)(
a) =
s(j)(
b) = 0
and
s(2m-1)(a) = 0
- Periodic interpolation
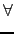
1
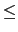 j
j 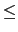
2
m - 1,
s(j)(
a) =
s(j)(
b)
A natural spline
is a spline function which verifies the natural interpolation constraints.
spline takes as arguments a list of abscissa (by increasing order),
a list of ordinates, a variable name, and a degree.
spline returns the natural spline function (with the specified degree
and crossing points) as a list of polynomials, each
polynomial being valid on an interval.
Examples:
- a natural spline of degree 3, crossing through the points
x0 = 0, y0 = 1,
x1 = 1, y1 = 3 and
x2 = 2, y2 = 0, input :
spline([0,1,2],[1,3,0],x,3)
Output is a list of two polynomial expressions of x :
[- 5*x3/4 + 13*x/4 + 1, 5*(x - 1)3/4 - 15*(x - 1)2/4 + (x - 1)/ - 2 + 3]
defined respectivly on the intervals [0, 1] and [1, 2].
- a natural spline of degree 4, crossing through the points
x0 = 0, y0 = 1,
x1 = 1, y1 = 3,
x2 = 2, y2 = 0 and
x3 = 3, y3 = - 1,
input :
spline([0,1,2,3],[1,3,0,-1],x,4)
Output is a list of three polynomial functions of x :
[(- 62*x4 + 304*x)/121 + 1,
(201*(x - 1)4 - 248*(x - 1)3 - 372*(x - 1)2 + 56*(x - 1))/121 + 3,
(- 139*(x - 2)4 + 556*(x - 2)3 + 90*(x - 2)2 + - 628*(x - 2))/121]
defined respectivly on the intervals [0, 1], [1, 2] and [2, 3].
- The natural spline interpolation of cos on
[0,
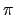 /2, 3
/2, 3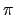 /2], input :
/2], input :
spline([0,pi/2,3*pi/2],cos([0,pi/2,3*pi/2]),x,3)
Output :
[((3*
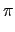
3 + (- 7*
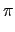
2)*
x + 4*
x3)*1/3)/(
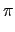
3),
((15*
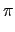
3 + (- 46*
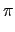
2)*
x + 36*
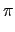
*
x2 - 8*
x3)*1/12)/(
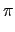
3)]





suivant: Arithmetic and polynomials
monter: Natural splines: spline
précédent: Theorem
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse