Smith normal form : ismith

ismith takes as argument a matrix with coefficients in $\mathbb {Z}$.
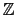ismith returns three matrices U,B and V such that B=U*A*V, U and V are invertible in 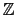$\mathbb {Z}$, B is diagonal, and B[i,i] divides B[i+1,i+1]. The coefficients B[i,i] are called invariant factors, they are used to describe the structure of finite abelian groups.
Input :

A:=[[9,-36,30],[-36,192,-180],[30,-180,180]]; U,B,V:=ismith(A)

Output :

[[-3,0,1],[6,4,3],[20,15,12]], [[3,0,0],[0,12,0],[0,0,60]], [[1,24,-30],[0,1,0],[0,0,1]]

The invariant factors are 3, 12 and 60.