 -
-
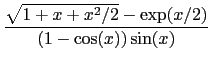
^2/2)-exp(x/2))/((1-cos(x))*sin(x)),x,0)
limit compute the limit of an expression in a finite or infinite point.
It is also possible with an optional argument to compute unidirectional
limit (1 for right limit and -1 for left limit .
limit takes three or four arguments :
an expression, the name of a variable (for example x), the limit point
(for example a) and an optional argument, by default 0, to
indicate if the limit is unidirectional.
This argument is equal to
-1 for a left limit (x<a) or is equal to 1
for a right limit (x>a) or is equal to 0 for a limite.
limit returns the limit of the expression when the variable (for example
x) approachs the limit point (for example a).
Remark
It is also possible to put x=a as argument instead of x,a, hence :
limit takes also as arguments an expression depending of a variable,
an equality (variable =value of the limit point) and perhaps 1 or -1 to
indicate the direction.
Input :
Exercises :
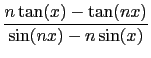
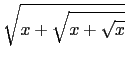 -
-
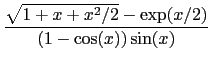
^2/2)-exp(x/2))/((1-cos(x))*sin(x)),x,0)
Remark
To compute limit, it is better sometimes to quote the first argument.
Input :