




suivant: Graph of a conic
monter: Quadratic forms
précédent: Reduction of a quadratic
Table des matières
Index
Gramschmidt orthonormalization : gramschmidt
gramschmidt takes one or two arguments :
- a matrix viewed as a list of row vectors,
the scalar product being the canonical
scalar product, or
- a list of elements
that is a basis of a vector subspace, and a function that defines a scalar
product on this vector space.
gramschmidt returns an orthonormal basis for this scalar product.
Input :
normal(gramschmidt([[1,1,1],[0,0,1],[0,1,0]]))
Or input :
normal(gramschmidt([[1,1,1],[0,0,1],[0,1,0]],dot))
Output :
[[(sqrt(3))/3,(sqrt(3))/3,(sqrt(3))/3],[(-(sqrt(6)))/6,(-(sqrt(6)))/6,(sqrt(6))/3],[(-(sqrt(2)))/2,(sqrt(2))/2,0]]
Example
We define a scalar product on the vector space of
polynomials by:
P.
Q =
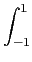 P
P(
x).
Q(
x)
dx
Input :
gramschmidt([1,1+x],(p,q)->integrate(p*q,x,-1,1))
Or define the function p_scal, input :
p_scal(p,q):=integrate(p*q,x,-1,1)
then input :
gramschmidt([1,1+x],p_scal)
Output :
[1/(sqrt(2)),(1+x-1)/sqrt(2/3)]
giac documentation written by Renée De Graeve and Bernard Parisse