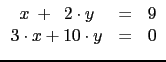



suivant: Construction of a Galois
monter: Computing in /p or
précédent: Inverse of a matrix
Table des matières
Index
Row reduction to echelon form in
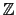 /p
/p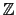 : rref
: rref
rref find the row reduction to echelon form of
a matrix with coefficients in
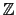 /p
/p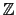 .
.
This may be used
to solve a linear system of equations with coefficients in
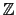 /p
/p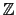 ,
by rewriting it in matrix form (see also 1.52.3) :
,
by rewriting it in matrix form (see also 1.52.3) :
A*X=B
rref takes as argument the augmented matrix
of the system (the matrix obtained by augmenting matrix A to the
right with the column vector B).
rref returns a matrix [A1,B1] : A1 has 1 on
it's principal diagonal, and zeros outside, and the
solutions in
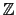 /p
/p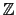 , of :
, of :
A1*X=B1
are the same as the solutions of:
A*X=B
Example, solve in
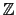 /13
/13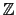
Input :
rref([[1, 2, 9]%13,[3,10,0]%13])
Or :
rref([[1, 2, 9],[3,10,0]])%13
Output :
[[1%13,0%13,3%13],[0%13,1%13,3%13]]
hence x=3%13 and y=3%13.
giac documentation written by Renée De Graeve and Bernard Parisse
![]() /p
/p![]() ,
by rewriting it in matrix form (see also 1.52.3) :
,
by rewriting it in matrix form (see also 1.52.3) :