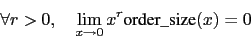
^n*order_size(x-a)
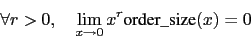
Examples :
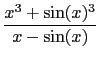 in the vicinity of x=0.
in the vicinity of x=0.
^3+sin(x)^3/(x-sin(x)))
^2+x^3*order_size(x)
^3+sin(x)^3/(x-sin(x)),x=0,7)
^3+sin(x)^3/(x-sin(x)),x,0,7)
^2+x^3+711/1400*x^4+
x^5*order_size(x)
^2,x=pi/6, 4)
^2+ 32*sqrt(3)/3/4*(x-pi/6)^3+(-16*3+16)/3/4*(x-pi/6)^4+ (x-pi/6)^5*order_size(x-pi/6)
^3+1/-5*(1/x)^5+
(1/x)^6*order_size(1/x)
^2*order_size(1/x)
^2+(1/x)^3*order_size(1/x)
^2+
^3*order_size(-1/x)
 in
the vicinity of x = 0+. Input :
in
the vicinity of x = 0+. Input :
^(1/x)/x^3,x=0,2,1)
^3+(-(exp(1)))/2/x^2+1/x*order_size(x)