



suivant: Orthogonal polynomials
monter: Arithmetic and polynomials
précédent: Sylvester matrix of two
Table des matières
Index
Resultant of two polynomials : resultant
resultant takes as argument two polynomials and
returns the resultant of the two polynomials.
The resultant of two polynomials is the determinant of their
Sylvester matrix S.
The Sylvester matrix S of two polynomials
A(x) = 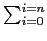 aixi
and
B(x) =
aixi
and
B(x) = 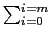 bixi
is a square matrix with m + n rows and columns; its first m rows
are made from the coefficients of A(X):
bixi
is a square matrix with m + n rows and columns; its first m rows
are made from the coefficients of A(X):
and the following n rows are made in the same way from the
coefficients of B(x) :
If A and B have integer coefficients with non-zero resultant r,
then the polynomials equation
AU + BV = r
has a unique solution U, V such that degree(U) <degree(B) and
degree(V) <degree(A), and this solution has integer coefficients.
Input :
resultant(x^3-p*x+q,3*x^2-p,x)
Output :
-4*p^3-27*q^2
Remark
discriminant(P)=resultant(P,P').
An example using resultant
Let, F1 and F2 be 2 fixed points in the plan and
A, a variable point on the circle of center F1 and radius 2a.
Find the cartesian equation of the set of points M, intersection of
the line F1A and of the segment bisector of F2A.
Geometric answer :
MF1 + MF2 = MF1 + MA = F1A = 2a
hence M is on an ellipse with focus F1, F2 and major axis 2a.
Analytic answer :
In the Cartesian coordinate system of center F1
and x-axis having the same
direction than the vector F1F2, the coordinates of A are :
A = (2
a cos(

);2
a sin(

))
where  is the (Ox, OA) angle.
Now choose
t = tan(
is the (Ox, OA) angle.
Now choose
t = tan( /2) as parameter, such that the coordinates
of A are rational functions with respect to t.
More precisely :
/2) as parameter, such that the coordinates
of A are rational functions with respect to t.
More precisely :
A = (
ax;
ay) = (2
a
;2
a
)
If F1F2 = 2c and if I is the midel point of AF2,
since the coordinates of F2 are F2 = (2c, 0), the coordinates
of I
I = (
c +
ax/2;
ay/2) = (
c +
a
;
a
)
IM is orthogonal to AF2, hence M = (x;y) verify the equation
eq1 = 0 where
eq1 : = (x - ix)*(ax - 2*c) + (y - iy)*ay
But M = (x;y) is also on F1A, hence M verify the equation eq2 = 0
eq2 : = y/x - ay/ax
The resultant of both equations with respect to t
resultant(eq1,eq2,t) is a polynomial eq3 depending on the
variables x, y, independant of t which is the cartesian equation
of the set of points M when t varies.
Input :
ax:=2*a*(1-t^2)/(1+t^2);ay:=2*a*2*t/(1+t^2);
ix:=(ax+2*c)/2; iy:=(ay/2)
eq1:=(x-ix)*(ax-2*c)+(y-iy)*ay
eq2:=y/x-ay/ax
factor(resultant(eq1,eq2,t))
Output gives as resultant :


The factor
 is always different from zero,
hence the locus equation of M :
is always different from zero,
hence the locus equation of M :
If the frame origin is O, the middle point of F1F2,
we find the cartesian equation of an ellipse.
To make the change of origin
 , input :
, input :
Output :
or if
b2 = a2 - c2, input :
Output :
that is to say, after division by a2*b2, M verifies the equation :

+

= 1
Another example using resultant
Let F1 and F2 be fixed points and A a variable point on the
circle of center F1 and radius 2a.
Find the cartesian equation of the hull of D, the segment bisector
of F2A.
The segment bisector of F2A is tangent to the ellipse of focus
F1, F2 and major axis 2a.
In the Cartesian coordinate system of center F1 and x-axis having the same
direction than the vector F1F2, the coordinates of A are :
A = (2
a cos(

);2
a sin(

))
where  is the (Ox, OA) angle.
Choose
t = tan(
is the (Ox, OA) angle.
Choose
t = tan( /2) as parameter, such that the coordinates of A are
rational functions with respect to t.
More precisely :
/2) as parameter, such that the coordinates of A are
rational functions with respect to t.
More precisely :
A = (
ax;
ay) = (2
a
;2
a
)
If F1F2 = 2c and if I is the middle point of AF2:
F2 = (2
c, 0),
I = (
c +
ax/2;
ay/2) = (
c +
a
;
a
)
Since D is orthogonal to AF2, the equation of D is
eq1 = 0 where
eq1 : = (x - ix)*(ax - 2*c) + (y - iy)*ay
So, the hull of D is the locus of M, the intersection point of D
and D' where D' has equation
eq2 : = diff (eq1, t) = 0.
Input :
ax:=2*a*(1-t^2)/(1+t^2);ay:=2*a*2*t/(1+t^2);
ix:=(ax+2*c)/2; iy:=(ay/2)
eq1:=normal((x-ix)*(ax-2*c)+(y-iy)*ay)
eq2:=normal(diff(eq1,t))
factor(resultant(eq1,eq2,t))
Output gives as resultant :


The factor
 is always different from zero,
therefore the locus equation is :
is always different from zero,
therefore the locus equation is :
If O, the middle point of F1F2, is choosen as origin,
we find again the cartesian equation of the ellipse :

+

= 1




suivant: Orthogonal polynomials
monter: Arithmetic and polynomials
précédent: Sylvester matrix of two
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
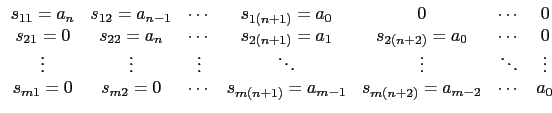
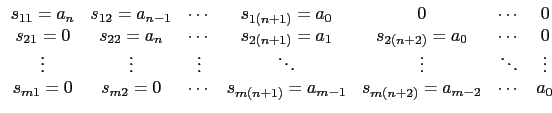
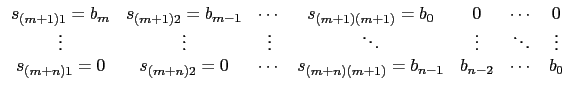
 ;2a
;2a )
)
 ;a
;a )
)
 ;2a
;2a )
)
 ;a
;a )
)