fourier_an

fourier_an takes four or five arguments : an expression expr depending of a variable, the name of this variable (for example x), the period T, an integer n and a real a (by default a = 0).
fourier_an(expr,x,T,n,a) returns the Fourier coefficient a_n of a function f of variable x defined on [a, a + T[ by f (x) = expr and such that f is periodic of period T:

a_n = $${\frac{{2}}{{T}}}$$$$\int_{a}^{{a+T}}$$f (x)cos($${\frac{{2\pi nx}}{{T}}}$$)dx

To simplify the computations, ons should input assume(n,integer) before calling fourier_an to specify that n is an integer.
Example Let the function f, of period T = 2, defined on [- 1;1[ by f (x) = x².
Input, to have the coefficient a₀ :

fourier_an(x^2,x,2,0,-1)

Output :

1/3

Input, to have the coefficient a_n (n 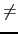$\neq$ 0) :

assume(n,integer);fourier_an(x^2,x,2,n,-1)

Output :

4*(-1)^n/(pi^2*n^2)