



suivant: Choosing the GCD algorithm
monter: Arithmetic and polynomials
précédent: GCD of two polynomials
Table des matières
Index
GCD of two polynomials with Euclide algorithm : Gcd
Gcd is the inert form of gcd.
Gcd returns the gcd (greatest common divisor) of two polynomials
(or of a list of polynomials or of a sequence of polynomials) without
evaluation. It is used when Xcas is in Maple mode to compute
gcd of polynomials with coefficients in
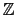 /p
/p using Maple-like syntax.
using Maple-like syntax.
Input in Xcas mode :
Gcd(x^3-1,x^2-1)
Output :
gcd(x^3-1,x^2-1)
Input in Maple mode :
Gcd(x^2+2*x,x^2+6*x+5) mod 5
Output :
1
giac documentation written by Renée De Graeve and Bernard Parisse