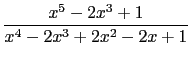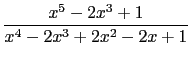Partial fraction expansion : partfrac

partfrac takes as argument a rational fraction.
partfrac returns the partial fraction expansion of this rational fraction.
The partfrac command is equivalent to the convert command with parfrac (or partfrac or fullparfrac) as option (see also 1.21.23).
Example :
Find the partial fraction expansion of :

$${\frac{{x^5-2x^3+1}}{{x^4-2x^3+2x^2-2x+1}}}$$

Input :

partfrac((x^5-2*x^3+1)/(x^4-2*x^3+2*x^2-2*x+1))

Output in real mode :

x+2-1/(2*(x-1))+(x-3)/(2*(x^2+1))

Output in complex mode:

x+2+(-1+2*i)/((2-2*i)*((i)*x+1))+1/(2*(-x+1))+

(-1-2*i)/((2-2*i)*(x+i))