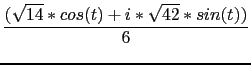



suivant: Graph of a quadric
monter: Quadratic forms
précédent: Graph of a conic
Table des matières
Index
Conic reduction : conique_reduite
conique_reduite takes two arguments : the equation of a conic
and a vector of variable names.
conique_reduite returns a list whose elements are:
- the origin of the conic,
- the matrix of a basis in which the conic is reduced,
- 0 or 1 (0 if the conic is degenerated),
- the reduced equation of the conic
- a vector of it's parametric equations.
Input :
conique_reduite(2*x^2+2*x*y+2*y^2+5*x+3,[x,y])
Output :
[[-5/3,5/6],[[-1/(sqrt(2)),1/(sqrt(2))],[-1/(sqrt(2)), -1/(sqrt(2))]],1,3*x^2+y^2+-7/6,[[(-10+5*i)/6+ (1/(sqrt(2))+(i)/(sqrt(2)))*((sqrt(14)*cos(` t`))/6+ ((i)*sqrt(42)*sin(` t`))/6),` t`,0,2*pi,(2*pi)/60]]]
Which means that the conic is not degenerated, it's reduced equation is
3x2 + y2 - 7/6 = 0
origin is
-5/3 + 5*i/6, axis are
parallel to the vectors (- 1, 1) and (- 1, - 1).
It's parametric equation is
where the suggested parameters value for drawing are
t from 0 to 2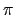 with tstep= 2
with tstep= 2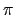 /60.
/60.
Remark :
Note that if the conic is degenerated and is made of 1 or 2 line(s),
the lines are not given by
their parametric equation but by the list of two points of the line.
Input :
conique_reduite(x^2-y^2+3*x+y+2)
Output :
[[(-3)/2,1/2],[[1,0],[0,1]],0,x^;2-y^2, [[(-1+2*i)/(1-i),(1+2*i)/(1-i)], [(-1+2*i)/(1-i),(-1)/(1-i)]]]




suivant: Graph of a quadric
monter: Quadratic forms
précédent: Graph of a conic
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse
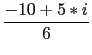 +
+ 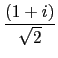 *
*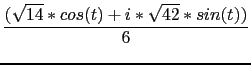
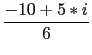 +
+ 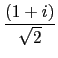 *
*