




suivant: The function : Zeta
monter: Real numbers
précédent: The function : Beta
Table des matières
Index
Derivatives of the DiGamma fonction : Psi
Psi takes as arguments a real a and an integer n (by
default n = 0).
Psi returns the value of the n-th derivative of the DiGamma function
at x = a, where the DiGamma fonction is the first derivative
of
ln(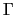 (x)). This function is used to evaluated sums of
rational functions having poles at integers.
(x)). This function is used to evaluated sums of
rational functions having poles at integers.
Input :
Psi(3,1)
Output :
pi^2/6-5/4
If n=0, you may use Psi(a) instead of Psi(a,0)
to compute the value of the DiGamma fonction at x = a.
Input :
Psi(3)
Output :
Psi(1)+3/2
Input :
evalf(Psi(3))
Output :
.922784335098
giac documentation written by Renée De Graeve and Bernard Parisse