Symbolic Algebra and Mathematics with XcasRenée De Graeve, Bernard Parisse1, |
© 2002, 2007 Renée De Graeve, Bernard Parisse
renee.degraeve@wanadoo.fr
bernard.parisse@ujf-grenoble.fr
User input in Xcas typically takes one of the following three forms:
| sin(pi/4) |
When describing command syntax, specific values that you enter for arguments are in typewriter font, while argument placeholders that should be replaced by actual values are in italics. Optional arguments will be enclosed by angular brackets. For example, you can find the derivative of an expression with the diff command (see Section 13.2.1), which takes the form diff(expr ⟨,x ⟩) where expr is an expression and x is (optionally) a variable or a list of variables.
In Xcas there exist many synonymous commands (i.e. having different names but the same effect). When a group of synonyms is described, the syntax details are provided only for the first command name and it is implied that the instructions apply to the synonyms as well.
In the index, the entries which are part of Xcas language are written in typewriter font (command names in black and programming keywords in blue) or italics (option names and specific values like color names).
The giac library is a C++ mathematics library. It comes with two interfaces use directly; a graphical interface and a command-line interface. All interfaces can do symbolic and numeric calculations, use giac’s programming language, and have a built in help function.
The graphical interface is called Xcas, and is the most full-featured interface. Xcas has additional help features to make it easy to use, plus it has a built-in spreadsheet, it can do dynamic geometry and it can do turtle graphics. The output given by this interface is typeset; for example:
| sqrt(2) |
|
The command-line interface can be run inside a terminal, and in a graphical environment can also draw graphs. The output given by this interface is in text form; for example:
| sqrt(2) |
There is also a web version, which can be run through a javascript-enabled browser (it works best with Firefox), either over the Internet or from local files. Other programs (for example, TeXmacs) have interfaces for the command-line version. Some of these interfaces, such as the two mentioned here, typeset their output.
The Xcas interface can run several independent calculation sessions, each session will be contained in a separate tab. Before you understand the Xcas interface, it would help to be familiar with the components of a session.
Each session can have any number of input levels. Each input level will have a number to the left of it; the number is used to identify the level. Each level can have one of the following:
You can enter a giac command (or a series of commands separated by semicolons) on a command line and send it to be evaluated by hitting enter. The result will then be displayed, and another command line will appear. You can also scroll through the command history with Ctrl+Up and Ctrl+Down.
If the output is a number or an expression, then it will appear in blue text in a small area below the input region; this area will be an expression editor (see Section 2.9). There will be a scrollbar and a small button M to the right of this area, which is a menu providing various options.
If the output is a graphic, then it will appear in a graphing area below the input region. To the right of the graphic will be a control panel which use to manipulate the graphic (see Section 19.1.1).
Levels can be moved up and down in a session, or even moved to a different session.
The level containing the cursor is the current level. The current level can be evaluated or re-evaluated by typing enter.
You can select a level (for later operations) by clicking on the number in the white box to the left of the level. Once selected, the box containing the number turns black. You can select a range of levels by clicking on the number for the beginning level, and then holding the shift key while you click on the number for the ending level.
You can copy the instructions in a range of levels by selecting the range, and then clicking the middle mouse button on the number of the target level.
When you first start Xcas, you get a largely blank window, as shown in Figure 2.1. The first row will consist of the main menus; you can save and load Xcas sessions, configure Xcas and its interface and run various commands with entries from these menus.
The second row will contains tabs; one tab for each session that you are running in Xcas. Each tab will have the name of its session, or Unnamed if the session has no name. The first time you start Xcas, there will be only one session, which will be unnamed.
The third row will contain various buttons.
When this shows real (for example), then Xcas will by default only find real solutions of equations. When this shows cplx, then Xcas will find complex solutions of equations. When this shows CPLX, then Xcas will regard variables as complex; for example, it won’t simplify re(z) (the real part of the variable z) to z. (See sections 2.5.5 and 2.5.6.)
This tells you whether angles, as in trigonometric arguments, are measured in radians or degrees. (See Section 2.5.3.)
This tells you how many significant digits will be used in floating point calculations. (See Section 2.5.1.)
This tells you what syntax Xcas will use. Xcas can be set to emulate the languages of Python, Maple, MuPAD, or the TI89 series of calculators. (See Section 2.5.2.)
Along the right hand side of the keyboard are some keys that can be used to change the keyboard.
The << and >> buttons scroll through menu items. Clicking on one of the menu buttons will perform the appropriate action or replace the menu items by its submenu items. When submenu items appear, there will also be a BACK button to return to the previous menu. Clicking on the home button returns the menu buttons to the main menu.
After the menu buttons is a var button. This replaces the menu buttons by buttons representing the variables that you have defined. After that is a cust button, which displays commands that you store in a list variable CST (see section 3.3.10).
The last button, X, closes the menu bar.
Xcas is an extensive program, but using it is simplified with several different ways of getting help. The help menu (see section 2.4.4) has several submenus for various forms of help, some of which are mentioned below.
The menus provide different ways to work with Xcas and its sessions, as well as ways of inserting functions and constants into the current session. Selecting a menu item corresponding to a function or constant brings up the help index (see section 2.3.3) with the chosen function or constant selected.
Xcas can export a session, or parts of a session, to typesetting languages such as LATEX and MathML.
If you enter a command into Xcas and press Enter, the result will appear in the output box below the input, colored in blue. Any messages generated during the computation will be shown in the box between the input and output, colored in green (the box is otherwise hidden). For example:
| integrate(a/(x+a)^2,x=0..inf) |
No checks were made for singular points of antiderivative -1/(x+a) for definite integration in [0,+infinity]
|
Note that line breaks in a command entry can be entered by pressing Shift+Enter.
You can enter expressions on the command line, but Xcas also has a built-in expression editor that use to enter expressions in two dimensions, the way they normally look when typeset. When you have an expression in the editor, you can also manipulate subexpressions apart from the entire expression.
Xcas can manage integers with unlimited precision, such as the following (see Section 12.1.1):
| factorial(100) |
|
Gaussian integers are numbers of the form a+ib, where a and b are in ℤ. For most functions in this section, use Gaussian integers in place of integers.
Note that complex numbers are also used to represent points in the plane (see Section 26.5.2). Some functions and operators which work on complex numbers also work on points.
An operator is an infixed function. For example, the arithmetic functions +, -, *, /, and ^ are operators. (See Section 7.3.2 and Section 7.4.1.)
Xcas can evaluate the trigonometric functions in either radians or degrees (see Section 8.3.2). It can also manipulate them algebraically.
Polynomials are represented by expressions or by lists of coefficients in decreasing power order. In the first case, for instructions requiring a main variable (like extended gcd computations), the variable used by default is x if not specified. For coefficients in ℤ/nℤ, use % n for each coefficient of the list or apply it to the entire expression defining the polynomial.
The way to compute over ℤ/pℤ or over ℤ/pℤ[x] depends on the syntax mode:
The representation is the symmetric representation: e.g. 11%13 returns -2%13.
The Maple commands are discussed in Section 11.9.
You can set Xcas to work in Maple mode rather than native Xcas mode (see Section 2.5.2).
A permutation p of size n is a bijection from {0,…,n−1} to itself and is represented by the list:
| [p(0),p(1),p(2),…,p(n−1)]. |
For example, the permutation p represented by [1,3,2,0] is the function from [0,1,2,3] to [0,1,2,3] defined by p(0)=1, p(1)=3, p(2)=2, p(3)=0.
A cycle c of size p, represented by the list [a0,…,ap−1] (0≤ ak≤ n−1), is the permutation such that
| c(ai)=ai+1 for 0≤ i≤ p−2, c(ap−1)=a0, c(k)=k otherwise. |
For example, the cycle c represented by the list [3,2,1] is the permutation c defined by c(3)=2, c(2)=1, c(1)=3, c(0)=0 (i.e. the permutation represented by the list [0,3,1,2]).
This section is limited to symbolic (or exact) solutions of differential equations. For numeric solutions of differential equations, see odesolve (Section 23.4.1). For graphic representation of solutions of differential equations, see plotfield (Section 19.9.1), plotode (Section 19.8.3) and interactive_plotode (Section 19.9.2).
Note that most matrix factorization algorithms are implemented numerically, only a few of them will work symbolically.
See Section 14.1.1 for different norms on vectors.
An isometry of ℝn is a distance-preserving map. In ℝ2, the isometries are made up of:
In ℝ3, the isometries are made up of:
An isometry is direct if it preserves orientation (it does not involve a reflection), otherwise it is indirect.
An n× n matrix A determines an isometry of the function f:ℝn→ℝn by f(x)=Ax) is an isometry. Such isometries fix the origin, so they cannot involve translation, can only rotate about the origin, and the line or plane of reflection will pass through the origin.
An isometry in ℝ2 can be characterized by:
An isometry in ℝ3 can be characterized by:
The augmented matrix of the system A X=b is either the matrix obtained by gluing the column vector b to the right of the matrix A (as with border(A,tran(b))), representing A X=b, or the matrix obtained by gluing the column vector −b to the right of the matrix A, representing A x−b=0.
Linear programming problems involve maximizing a linear functionals under linear equality or inequality constraints. The simplest case can be solved directly by the so-called simplex algorithm. Most cases require you to solve an auxiliary linear programming problem to find an initial vertex for the simplex algorithm.
Let Γ be a curve in space parameterized by a continuously differentiable function, and M0 be a point on the curve. The curve will have an arclength parameterization; namely, it can be parameterized by a function M(s), where M(0)=M0 and |s| is the length of the curve from M0 to M(s), in the direction of the curve if s>0 and the opposite direction if s<0.
For such a Γ, the vector T(s)=M′(s) will be the unit tangent to the curve at M(s), and N(s)=T′(s) will be perpendicular to the tangent. The circle through M(s) with center at M(s)+N(s) is called the osculating circle to Γ at M(s). Informally, the osculating circle is the circle through M(s) which most closely approximates Γ. The set of all centers of curvature is another curve, called the evolute of Γ.
The radius of the osculating circle is |N(s)| and is called the radius of curvature of Γ at M(s). The reciprocal of this is called the curvature of Γ at M(s).
A curve can be described in Xcas with a parametrization or with a curve object. Various curve objects are described in chapters 26 and 27. The commands in this section can work with curves described either way. You can get the equation of a curve object with the equation command (see Section 26.12.7).
Most graph instructions take expressions as arguments. A few exceptions (mostly Maple-compatibility instructions) also accept functions. Some optional arguments, like color, thickness, can be used as optional attributes in all graphic instructions. They are described below.
The plotimplicit or implicitplot command draws curves or surfaces defined by an implicit expression or equation. If the option unfactored is given as the last argument, the original expression is taken unmodified. Otherwise, the expression is normalized, then replaced by the factorization of the numerator of its normalization.
Each factor of the expression corresponds to a component of the implicit curve or surface. For each factor, Xcas tests if it is of total degree less or equal to 2, in which case conic or quadric is called. Otherwise the numeric implicit solver is called.
Optional step and ranges arguments may be passed to the numeric implicit solver, note that they are dismissed for each component that is a conic or a quadric.
The plotparam or paramplot or DrawParm command draws parametric curves and surfaces.
Xcas can display animated 2D, 3D or “4D” graphs. This is done first by computing a sequence of graphic objects, then after completion, by displaying the sequence in a loop. To stop or start the animation, click on the button ▸ (to the left of Menu).
Xcas has several functions to perform statistics. Data is typically given as a list of numbers, such as A:=[0,1,2,3,4,5,6,7,8,9,10,11]. This particular list will be used in several examples. Statistics on matrices are discussed in Section 14.5.2.
Clustering is a form of unsupervised machine learning. Xcas can perform hierarchical clustering and k-means clustering.
This section explains how to create and train feed-forward neural networks in Xcas.
A feed-forward network, more precisely a multilayer perceptron, is comprised of a sequence of at least three neuron layers. The first layer is called the input layer and the last layer is called the output layer. Layers are essentially vectors of numerical data. Each component of such vector corresponds to an activated neuron. The network processes the given input by applying the formula lk+1=fk(WkTlk), where lk is the kth layer of length nk, lk+1 is the (k+1)-th layer of length nk+1, Wk is a nk× nk+1 weight matrix and fk is the activation function at the k+1-th layer (which is applied element-wise). Here k=1,2,…,L−1, where L is the number of layers. Each layer except the final one contains a bias neuron with linear activation. Bias neurons are auxiliary neurons created during construction of the network.
Multilayer perceptrons are trained by using backpropagation to compute the approximate gradient (with respect to the weight parameters in the matrices Wk) of the error function which compares the output to the expected output (or ground truth). Precisely, after training data is fed to the network, the obtained output is compared to the expected output and finally the error is backpropagated to find the weight adjustment enabling the network to predict the expected output more accurately.
The examples in Section 22.2.2 demonstrate how to prepare training data, construct neural networks, train them and test their accuracy.
The commands in this section require that giac is linked to GSL.
Real numbers may have an exact representation (e.g. rationals, symbolic expressions involving square roots or constants like π, …) or approximate representation, which means that internally the real is represented by a rational (with a denominator that is a power of the basis of the representation) close to the real. Inside Xcas, the standard scientific notation is used for approximate representation; that is a mantissa (with a point as decimal separator) optionally followed by the letter e and an integer exponent.
Note that, for example, the real number 10−4 is an exact number but 1e–4 is an approximate representation of this number.
This section discusses how real numbers are represented.
Numeric Cholesky, QR, LU, and SVD factorizations of a matrix can be carried out, as described in Section 15.3.
Xcas has a programming language that allows you to write complex programs in several different syntax flavours. This section explains the details of the language, how to enter programs in Xcas (most notably new functions) and how to debug them. In the end, it is briefly explained how to extend and use giac from C++.
Variables should be unspecified to demonstrate a general geometric result, but need to have specific values when drawing. There are a couple of different approaches to deal with this.
One approach is to use the assume command (see Section 3.3.8). If a variable is assumed to have a value, then that value will be used in graphics but the variable will still be unspecified for calculations. For example:
| assume(a=2.1):; A:=point(a+i) |
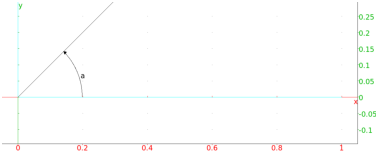
but the variable a will still be treated as a variable in calculations:
| distance(0,A) |
|
Another approach would be to use the point or pointer mode in a geometry screen. If no geometry screen is shown, the command Alt+G or the Geo ▸ New figure 2d menu will open a screen. Clicking on the Mode button right above the graphic screen and choosing pointer or point will put the screen in pointer or point mode. If a point is defined and displayed, such as with A:=point(2.1+i), then clicking on the name of the point (A in this case) with the right mouse button will bring up a configuration screen. As long as there is a point defined with non-symbolic values, there will be a symb box on the configuration screen. Selecting the symb box and choosing OK will be equivalent to the commands:
| assume(Ax=[2.1,-8.16901408451,8.16901408451]); assume(Ay=[1,-5.0,5.0] |
This brings up two lines beneath the arrows to the right of the screen which can be used to change the assumed values of Ax and Ay. Also, the point A will be redefined as point(Ax,Ay) (see Figure 26.1).
See Section 27.6 for triangles in space.
See Section 27.7 for quadrilaterals in space.
See Section 27.8 for polygons in space.
See also sections 27.4.6 and 27.4.7 for planes perpendicular and orthogonal to lines and planes.
See Section 26.8 for quadrilaterals in the plane.
See Section 26.9 for polygons in the plane.
To specify a Platonic solid, Xcas works with the center, a vertex and a third point to specify a plane of symmetry. To speed up calculations, it may be useful to use approximate calculations, which can be ensured with the evalf command. For example, instead of:
| centered_cube([0,0,0],[3,2,1],[1,1,0]) |
it would typically be better to use:
| centered_cube(evalf([0,0,0],[3,2,1],[1,1,0])) |
since it is faster.
Xcas has support for audio objects in wav (Waveform Audio File) format. The following commands are provided for working with audio objects.
|
|
This document was translated from LATEX by HEVEA.