- black, white, red, blue, green, magenta, cyan, yellow,
- a numeric value between 0 and 255,
- a numeric value between 256 and 256+7*16+14 for a color of the rainbow,
- any other numeric value smaller than 65535, the rendering is not guaranteed to be portable.
- rhombus_point plus_point
- square_point cross_point
- triangle_point
- star_point
- point_point
- invisible_point
- Point width, set with display=value. The
values can be:
point_width_n where n is an integer between 1 and 7. - Line thickness, set with thickness=n or display=line_width_n where n is an integer between 1 and 7.
- Line shape, set with display=value. The
values can be:
- dash_line
- solid_line
- dashdot_line
- dashdotdot_line
- cap_flat_line
- cap_square_line
- cap_round_line
- Legend, the text is set with
legend="legendname";
the position is set with display=value, where
the values can be:
- quadrant1
- quadrant2
- quadrant3
- quadrant4
- display=filled specifies that surfaces will be filled,
- gl_texture="picture_filename" is used to fill a surface with a texture. Cf. the interface manual for a more complete description and for gl_material= options.
Examples.
(See Section 13.10.3, Section 13.6.2,
Section 13.3.3 and Section 13.7.3 for information on
the commands used.)
-
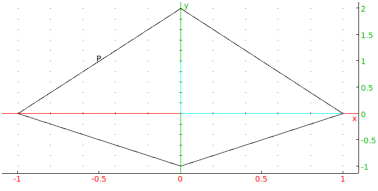
Input:
polygon(-1,-i,1,2*i,legend="P")Output:
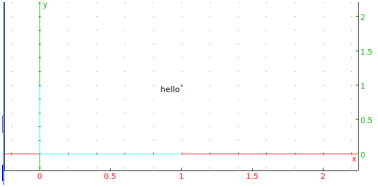
- Input:
point(1+i,legend="hello")Output:
- Input:
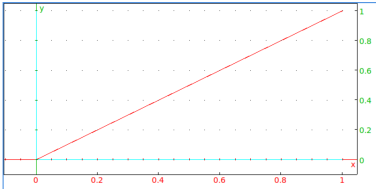
color(segment(0,1+i),red)Output:
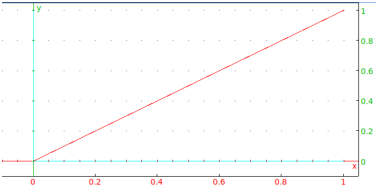
- Input:
segment(0,1+i,color=red)Output: