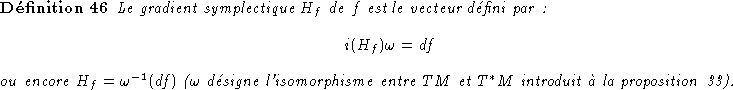
En coordonnées canoniques, on a:
![]()
En effet, si Hf a pour coordonnées:
![]()
et si ![]() a pour coordonnées:
a pour coordonnées:
![]()
comme ![]() ,
,
![]()
donc:
![]()
d'où:
![]()
Pour intégrer le système d'équations (16), on peut alors
chercher une transformation canonique qui le simplifie (i.e. qui ramène f
à une forme dite normale, par exemple on ramène localement
f à ![]() si f n'est pas critique, où (sur
si f n'est pas critique, où (sur ![]() )
à une fonction
de
)
à une fonction
de ![]() si f admet un minimum non dégénéré, ...)
On a en effet la:
si f admet un minimum non dégénéré, ...)
On a en effet la:
Autrement dit, pour déterminer la trajectoire du flot hamiltonien (i.e. intégrer (16)) dans les nouvelles coordonnées, il suffit d'écrire les équations (16) en remplaçant f par son expression en fonction des nouvelles coordonnées.
Preuve:
On a:
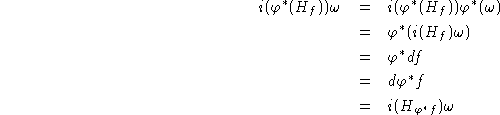
On conclut parce que ![]() est non dégénérée.
est non dégénérée.
Exemple:
Considérons dans ![]() muni de
muni de ![]() , le
hamiltonien
, le
hamiltonien ![]() . Les équations du flot hamiltonien
s'écrivent:
. Les équations du flot hamiltonien
s'écrivent:
![]()
Pour les intégrer, il est nécessaire de les combiner en une
équation du second ordre en x par exemple.
Effectuons plutôt la tranformation canonique:
![]()
qui est canonique car linéaire de déterminant 1. Le hamiltonien
s'écrit dans les nouvelles coordonnées, ![]() . L'équation
du flot devient donc:
. L'équation
du flot devient donc:
![]()
on a découplé le système en deux équations du premier ordre
ce qui est beaucoup plus agréable (même si dans cet exemple
précis, on sait résoudre explicitement les deux systèmes).
Trouver une bonne transformation canonique est souvent profitable
non seulement en mécanique classique mais aussi en mécanique
quantique.
Preuve:
Commençons par déterminer la dérivée en t=0 de
![]() :
:
![]()
d'après la formule de Cartan (14),
puis on applique ![]() (car M symplectique) et
(car M symplectique) et
![]()
ce qui donne:
On en déduit que ![]() . En effet, le système
différentiel:
. En effet, le système
différentiel:
![]()
admet une solution unique et l'équation (17) montre que
![]() est solution.
est solution.
On en déduit immédiatement la:
On remarque également que:
![]()
d'où la: