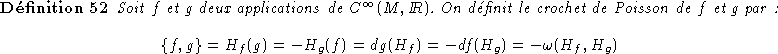
Par exemple, en dimension 1, savoir que le hamiltonien lui-même est conservé permet de dire que les courbes intégrales du flot se confondent avec les lignes de niveau du hamiltonien. Donnons un autre exemple en dimension 2. Supposons que le hamiltonien f est invariant par rotation, par exemple prenons:
Alors, on a 
, et comme
la partie du crochet de Poisson de f et de
où l'ondérive f par rapport à
x et y est nulle. On s'aperçoit alors
que la deuxième partie (celle où on dérive f par rapport à
et 
) est également nulle, on en déduit la
conservation de g, c'est-à-dire la conservation du moment cinétique.
Les deux premières propriétés sont évidentes, montrons la troisième. On a:
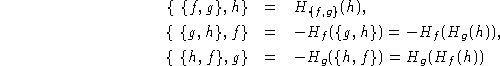
on est ramené à montrer que:
ou encore que:
Preuve:
On effectue la dérivée de Lie par rapport à Hf de l'identité
ce qui donne pour le membre de gauche:
et pour le membre de droite, en appliquant (15):
d'après (17) d'où:
ce qu'il fallait démontrer.
Remerciements.
Je remercie Yves Laurent de m'avoir proposé de donner ce cours, Frédéric Faure pour ses suggestions (en particulier la visualisation du dual d'un espace vectoriel) et Laurent Stolovitch pour sa patiente relecture de ces notes.
