Application à un potentiel périodique sur un réseau.

  Il s'agit ici de corriger une erreur dans notre article [2] (voir l'erratum). On considère la situation suivante:

• V est un potentiel périodique sur un réseau de :

  

  On notera F un domaine fondamental de périodicité de V.

• V est ,
• ,
• V admet un seul puits non dégénéré par cellule de périodicité, on supposera quitte à changer d'origine, que est l'ensemble des puits. On suppose aussi qu'on a choisi le domaine F de telle sorte que O soit le centre de F.

Soit le réseau dual de et soit . Soit l'ensemble des fonctions de L²(F) qui se prolongent en une fonction sur vérifiant les conditions de périodicité:

Alors l'opérateur défini sur par l'action de D_V(h) admet un spectre discret et le spectre de D_V(h) est la réunion, lorsque parcourt de ces spectres.

On s'intéresse maintenant à la partie du spectre de D_V(h) proche de E=0. Considérons le problème à un puits D₁ obtenu à partir de D_V en ``bouchant'' tous les puits de potentiels de V sauf celui situé à l'origine (en pratique, on définit un potentiel égal à V sauf sur des boules de taille centrées sur où l'on augmente [respectivement diminue] si V(0)=-1 [respectivement V(0)=1]). Soient u₁ et u₂=Ku₁ une base de fonctions propres de D₁ correspondant à une énergie et soit une troncature à support compact dans F et valant 1 dans un voisinage de l'origine. Alors et forment un couple de quasi-modes indépendants de de quasi-énergie E_n(h). Ceci montre que le spectre de ne dépend que de manière exponentiellement faible de . Le spectre de D_V au voisinage de E=0 est donc constitué de bandes de largeur exponentiellement petite. Il est alors naturel:

• de déterminer la taille de ces bandes,
• de voir si une valeur propre double de D₁ donne deux valeurs propres distinctes de .

Pour cela, il suffit d'améliorer nos quasi-modes et puis de diagonaliser la matrice de D-E_n(h) dans cette base de quasi-modes.

Soit S la distance d'Agmon minimale entre deux points du réseau . On construit une nouvelle fonction de troncature telle que:

• si , où est fixé,
• si .

Pour fixer les idées, on peut observer que si les distances d'Agmon latérales, longitudinales et verticales du réseau sont du même ordre de grandeur, sur F , alors que sur . On ne peut plus prendre et comme quasi-modes car ils ne sont pas -Floquet périodiques (ci-dessus ils l'étaient car ils étaient nuls au bord de F). On les périodise donc en posant pour j=1,2:

Pour x fixé, la somme sur est en fait finie car est à support compact. Comme on va le voir, les effets d'interactions sont de l'ordre de e^-S/h. On va donc adopter la notation pour dire que:

• deux réels sont égaux à une erreur d'ordre exponentiellement petite devant e^-S/h:

  

• deux fonctions sont égales (au sens L² ou H¹) à une erreur d'ordre exponentiellement petite devant e^-S/2h (le coefficient 2 vient du fait que les réels sont construits en calculant des normes au carré ou des produits scalaires).

Supposons pour fixer les idées que les deux points les plus proches de O pour la distance d'Agmon soient et : cf. figure 1, p. . Plus loin, on notera simplement et qui désignera donc selon le contexte un point ou un réel. Alors, sur F, on a:

Les valeurs propres de la matrice d'interaction sont donc équivalentes au sens ci-dessus aux . Comme sur F, on a:

on en déduit:

  
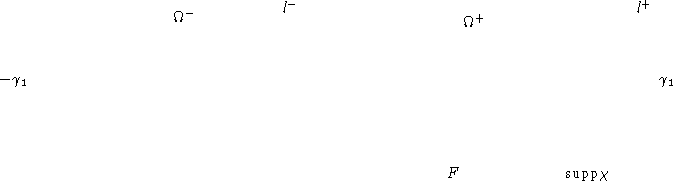
Figure 1: Calcul de la matrice d'interaction.

Supposons qu'il existe une unique géodésique l⁺ reliant O à . Alors la première intégrale est équivalente (au sens ci-dessus) à l'intégrale sur un voisinage de l'intersection de l⁺ et du support de . De même, la deuxième intégrale est équivalente à l'intégrale sur un voisinage de l'intersection du translaté l^- par de l⁺ et du support de .

Pour évaluer ces deux intégrales, l'idée est de faire passer D-E_n(h) de l'autre côté, en utilisant le fait que D est formellement autoadjoint. Il ne restera alors que des termes de bord sur et puisque (D-E_n(h))u_k=0. On évalue alors ces termes de bord en remplaçant les fonctions par leurs approximations BKW et en appliquant le théorème de la phase stationnaire, ce qui suppose une hypothèse de non-dégénérescence de la géodésique l⁺. Le terme (j,k) de la matrice d'interaction vaut alors d'après le théorème de Stokes:

où désigne la normale extérieure à exprimée dans la base et u^BKW_j,P désigne la solution BKW correspondant à u_j issue du point P.

Soit . Sur la géodésique l⁺, on a d⁺(x)=S et . On suppose que l⁺ est non dégénérée, c'est-à-dire que la hessienne transversale de d⁺ est définie positive le long de l. Comme le terme exponentiel par rapport à h dans l'intégrale sur est justement e^{-d<<1353>>+(x)/h}, le lemme de la phase stationnaire montre que le terme (j,k) de la matrice d'interaction admet un développement semi-classique dont le terme principal est:

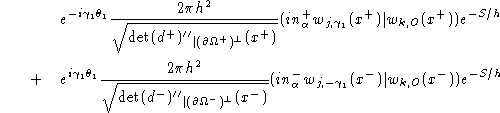
où désigne le point de tel que et w_j,P désigne le symbole principal de la solution BKW issue de P correspondant à u_j (c'est le terme w₀ dans (4).

Pour utiliser la périodicité, on aimerait que . On choisit donc et de telle sorte que et (comme sur la figure). On obtient alors pour le terme (j,k):

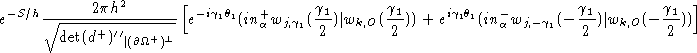
Pour faire le lien avec les sections précédentes, il faut exprimer des termes de la forme

en fonction du vecteur tangeant à la géodésique. En fait:

ne dépend pas de la direction de n⁺ mais uniquement du sens (sortant ou entrant). En effet, si l'angle entre n⁺ et le vecteur tangeant à la géodésique est , on a:

(on le voit facilement en faisant un changment de coordonnées dans le plan engendré par n⁺ et t, et en faisant un développement limité à l'ordre 2 de (d⁺) '' en x⁺ ).

D'autre part, si n est un vecteur orthogonal à la géodésique, alors on applique (31):

donc:

On peut donc supposer que est le vecteur tangent à l⁺ orienté dans le sens des x₁ décroissants et le vecteur tangent à l^- orienté dans le sens des x croissants. Par périodicité, on a:

En utilisant le fait que u₂=Ku₁ et les propriétés de l'opérateur de Kramers K, on montre que la matrice d'interaction est:

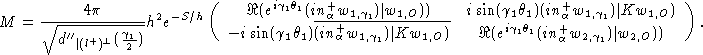
Les valeurs propres de M sont les:

où:

 

Finalement les valeurs propres sont:

 

La bande de spectre centrée autour de E_n(h) n'est donc pas double génériquement. En fait, chaque valeur propre ou parcourt la même bande avec un déphasage par rapport à l'autre valeur propre.