Le cas général.

  On considère donc le symbole principal w₀ d'une fonction propre:

 

associée à E_n(h). On écrit l'équation:

et on décompose en puissances croissantes de h (cf. [5] et [3, p. 1099,] pour plus de détails). La première puissance de h donne:

 

ce qui entraîne que 0 est valeur propre de la matrice , condition qui se traduit par l'équation éïconale:

En d'autres termes, d est la distance d'Agmon associée à la métrique (1-V²)dx². La deuxième puissance de h donne l'équation de transport:

 

où s désigne l'abscisse curviligne euclidienne le long de la géodésique d'Agmon. On retrouve ici le premier terme du développement asymptotique de E_n(h) dans (3) en faisant s=0. Si on note , on a:

 

Rappelons que le comportement de w₀(x) au voisinage de l'origine est:

 

où x(s)ⁿ=x₁^n₁ x₂^n₂ x₃^n₃ dans des coordonnées qui diagonalisent V''(0).

On commence par traiter la partie non différentielle scalaire. On est naturellement amené à faire le changement de variable:

 

la fonction vectorielle y doit alors satisfaire l'équation:

 

Ce changement de variables n'est pas valide lorsque car l'intégrale de (9) diverge. On peut néanmoins contrôler cette divergence. On fixe t (t est censé être petit devant s) et on pose:

 

on ajoute ici le coefficient constant (par rapport à s) x(t)ⁿ ce qui permet de faire tendre t vers 0. En effet, si on considère la fonction:

on observe que:

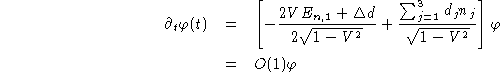
La fonction y satisfait toujours à l'équation (10). Enfin, lorsque t tend vers 0, les remarques précédentes montrent que y(0) tend vers la constante C de (8).

On peut résumer les résultats obtenus par la: