Xcas/χ\chicas: calcul formel et algorithmitique.
À la conquête des calculatrices et du web!

Bernard.Parisse@univ-grenoble-alpes.fr

2019

Table des matières

1  Introduction

Les nouveaux programmes de lycée ont introduit des nouveautés en algorithmique, avec l’accent mis sur la notion de fonction et l’utilisation de Python comme langage de programmation. Cela ne doit pas faire oublier que l’utilisation de logiciels de calcul numérique, calcul formel et représentation graphique conserve toute sa place dans les programmes de mathématiques : on lit dans le préambule des programmes de 1ere, Terminale
L’utilisation de logiciels (calculatrice ou ordinateur), d’outils de visualisation et de représentation, de calcul (numérique ou formel), de simulation, de programmation développe la possibilité d’expérimenter, favorise l’interaction entre l’observation et la démonstration et change profondément la nature de l’enseignement. L’utilisation régulière de ces outils peut intervenir selon trois modalités :

Ces deux dernières années, une bonne partie du développement de Xcas a eu pour objectif de couvrir l’ensemble de ces thèmes au sein du même logiciel, de l’algorithmique en langage naturel ou en syntaxe Python, du calcul numérique et formel et des représentations graphiques, et ce sur une grande variété de plateformes matérielles: ordinateurs (et dans une moindre mesure tablettes ou smartphones), mais aussi calculatrices graphiques de milieu de gamme (Casio, Numworks) dont l’importance en milieu scolaire est grande en raison de sa souplesse d’utilisation.

Dans la section 2, nous présentons les aspects calcul formel, la section 3 sera consacrée à l’algorithmique pour l’enseignement, nous y montrerons comment utiliser Xcas comme plateforme de programmation compatible Python au lycée, la section 4 présente plusieurs plateformes matérielles où on peut installer Xcas, en particulier calculatrices, avec leurs particularités et limites.

2  Calcul formel

Le calcul formel est la fonctionnalité principale de Xcas, ainsi que ses interactions, en particulier la géométrie analytique exacte. Comme dans tout système de calcul formel, la possibilité d’étendre le système en programmant de nouvelles commandes, avec le langage utilisateur (ou pour les experts par des modules dynamiques écrits en langage compilé).

Le menu outil de Xcas permet de trouver efficacement les commandes les plus utilisées, par thèmes : résolution d’équations et systèmes, calcul différentiel et intégral, simplifications, arithmétique, algèbre linéaire, probabilités. Les autres sont dans le menu Cmds, ou Graphes. Un menu spécifique est prévu pour écrire des programmes (avec des assistants pour créer une fonction, un test ou une boucle), construire une figure de géométrie (2d/3d), ou saisir une matrice ou un tableur formel. Lorsqu’on sélectionne une commande depuis le menu, l’index de l’aide en ligne rapide apparait à cette commande, avec une description courte et des exemples qu’il suffit en général de recopier et modifier. En cliquant sur le bouton Details, l’aide plus complète apparait dans une fenêtre du navigateur. La prise en main est en général rapide, voici un exemple d’ énoncé de début de 1ère année de licence, parcours physique, en 1 heure les étudiants arrrivent à l’exercice 6, et un énoncé de 2ème année de licence, parcours physique, dont la partie TP de prise en main se fait en 1h30 environ. Les difficultés principales rencontrées sont le parenthésage et l’utilisation de la multiplication implicite entre deux variables, par exemple entre ii et π\pi (ipi au lieu de i*pi, ou xy au lieu de x*y).

Dans l’enseignement, Xcas peut servir d’outil de vérification. La vérification est un aspect souvent négligé par les élèves et étudiants ou alors ils s’en remettent à l’enseignant, sans tester par eux-mêmes avec d’autres approches (représentation graphique, essai pour des valeurs particulières de paramètres, calcul symbolique avec du calcul formel). Dans les cas trop techniques (“trop” dépend bien sur de l’élève), faire faire le calcul au logiciel peut permettre de comprendre des concepts qui seraient sinon noyés dans les difficultés rencontrées pour mener à bien les calculs à la main. Bien entendu, il faut continuer à faire du calcul mental et du calcul littéral à la main, mais il faut aussi savoir se servir d’un logiciel de calcul formel et l’utiliser à bon escient.

Un autre intérêt de Xcas est de permettre de faire des preuves assistées. Xcas peut servir, comme d’autres logiciels non formel, d’aide à la conjecture, que l’on démontre ensuite papier-crayon. En géométrie analytique, on peut faire des calculs exact et avec des paramètres, ce qui permet de fournir une preuve par le logiciel de certains théorèmes, preuve que l’on peut bien sur compléter par une preuve en géométrie synthétique. 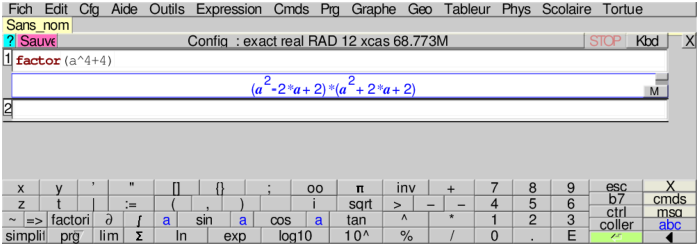Enfin, on peut se servir de Xcas comme d’une boule de cristal. Par exemple si on souhaite déterminer les entiers a≥1a\geq 1 tels que a 4+4a^4+4 est premier, la factorisation de a 4+4a^4+4 est hors de portée d’un élève de lycée, mais il peut vérifier en développant à la main la factorisation calculée par le logiciel.

D’autres activités du même type sont en cours de développement par le groupe Preuve par le calcul formel de l’IREM de Grenoble.

3  Algorithmique et programmation

Comprendre un algorithme, c’est souvent difficile, le programmer, c’est à la fois plus difficile mais aussi source de satisfaction quand on a écrit un programme qui fonctionne, ce qui peut motiver des élèves par ailleurs peu intéressés par les maths. Enseigner l’algorithmique et la programmation est d’autant plus délicat si on n’est pas soi-même à l’aise et qu’on ne dispose pas d’une formation permanente à la hauteur de l’enjeu. On risque de déclarer faux un algorithme correct, et surtout on risque de se trouver en situation de grand stress pendant une séance de TP si on n’arrive pas à débloquer rapidement des élèves devant une erreur de syntaxe ou d’exécution (en général on se retrouve devant une dizaine de M’sieur ça marche pas, puis tous les élèves se démotivent). Avoir des objectifs trop ambitieux, c’est courir le risque de voir se reproduire ce qui s’est passé avec les maths modernes ou plus récemment les statistiques inférentielles. On risque de voir se multiplier des séances de bachotage où l’enseignant écrit en début de séance un programme tout fait au tableau, que les élèves sont invités à recopier religieusement, avec des formules rituelles mal comprises (par exemple from math import *). Il importe donc de bien distinguer l’algorithme que l’on pourra traduire essentiellement dans tout langage de programmation et le programme avec les spécificités de syntaxe de Python (pas toujours heureuses), il ne faut pas oublier que d’autres langages de programmation populaires existent aujourd’hui (par exemple Javascript) et que dans 10 ou 20 ans, un autre langage de programmation aura peut-etre supplanté Python chez les scientifiques qui l’utilisent aujourd’hui (le langage Julia par exemple). L’algorithme en langage naturel est beaucoup plus pérenne, il se prête aussi mieux à une analyse mathématique (y-a-t-il un invariant de boucle ? quel est le nombre d’itérations de cette boucle ? est-on bien sur qu’il se termine ?), c’est d’ailleurs en langage naturel que les algorithmes sont présentés dans les articles de recherche en calcul formel ou les références d’algorithmique, comme par exemple la référence en livre numérique pour l’algorithmique de l’agrégation interne. C’est enfin le langage qui se prête le mieux à une évaluation papier-crayon, comme c’est le cas actuellement au bac, espérons que cela ne changera pas.

Comme les programmes scolaires imposent Python comme langage de programmation, il faut bien sur utiliser une syntaxe compatible avec Python lorsqu’on écrit un programme, mais j’espère avoir convaincu qu’il ne faut pas être intégriste, utiliser Xcas en syntaxe compatible Python est tout à fait conforme aux programmes de maths et présente plusieurs avantages pour l’enseignement des mathématiques par rapport à un environement Python natif :

D’un point de vue progression, il me parait raisonnable d’avoir comme premier objectif, avant d’écrire une fonction, d’être capable d’écrire une ligne de commande de shell, pour maitriser un minimum les règles d’écriture (priorité de + et *, parenthésage, appel de fonctions usuelles). C’était indispensable sur les calculatrices auparavant, mais plus maintenant avec la généralisation de la saisie en écriture naturelle (ou 2d), sauter cette étape risque d’augmente la difficulté du passage à la programmation. On peut ici utiliser la calculatrice en passant en mode de saisie algébrique. Si on a un logiciel de calcul formel ou une calculatrice formelle cela peut motiver les élèves, car ils pourront vérifier des développements et factorisations.

On peut ensuite faire des définitions de fonction algébriques, par exemple le maximum en valeur absolue de 2 puis de 3 réels. 

def maxabs2(a,b):
    return max(abs(a),abs(b))
def maxabs3(a,b,c):
    return max(maxabs2(a,b),abs(c))

onload

Avec la tortue, on peut introduire la notion de suite d’intructions, puis de fonctions dans un contexte non algébrique. On peut commencer par faire tracer un carré instruction par instruction depuis le shell puis regrouper en un programme, 

def Carre():
  avance(20)
  tourne_gauche
  avance(20)
  tourne_gauche
  avance(20)
  tourne_gauche
  avance(20)
  tourne_gauche

puis simplifier à l’aide d’une boucle 

def Carre():
  for j in range(4):
    avance(20)
    tourne_gauche

onload

puis passer en paramètre la longueur, puis le nombre de cotés d’un polygone régulier 

def polyg1(l,n):
  for j in range(n):
     avance(l)
     tourne_gauche(360.0/n)

onload

et par exemple finir par construire tous les polygones réguliers de 3 à nn cotés :

Une approche alternative consiste à travailler en géométrie analytique. On commence par définir deux points AA et BB. Puis on calcule les abscisses de AA et de BB, les ordonnées de AA et BB, les coordonnées du milieu de AA et BB, et on construit le point milieu. 

# construction du milieu de 2 points
A=point(1,3)
B=point(-2,2)
Ax=abscisse(A)
Bx=abscisse(B)
Ay=ordonnee(A)
By=ordonnee(B)
Mx=(Ax+Bx)/2
My=(Ay+By)/2
M=point(Mx,My)

onload
On passe alors à la définition de fonction prenant en argument les deux points AA et BB et renvoyant le point MM, milieu de AA et BB : 

def Milieu(A,B):
  Ax=abscisse(A)
  Bx=abscisse(B)
  Ay=ordonnee(A)
  By=ordonnee(B)
  Mx=(Ax+Bx)/2
  My=(Ay+By)/2
  return point(Mx,My)

onload

On peut aussi calculer l’équation de la droite ABAB, chercher l’intersection de deux droites, construire le centre du cercle circonscrit, etc. Le manuel Algorithmique au lycée de Xcas contient beaucoup d’exemples de ce type.

On peut ensuite passer à des squelettes de fonction plus ambitieuses à compléter par exemple pour la recherche de longueur approchée de courbe et du minimum d’une expression. Notre groupe IREM de Grenoble propose trois TP pour l’enseignement de l’algorithmique en seconde avec Xcas, écrits en langage naturel avec des traductions en Python. Le troisième énoncé recherche d’un extremum, illustre comment on peut proposer de faire modifier un programme existant, sans que les élèves ne perdent du temps à recopier un programme au tableau avec risques d’erreur de recopie.

4  Où utiliser Xcas/χ\chicas.

Le moteur de calcul de Xcas, Giac, est utilisable par l’intermédiaire de nombreuses interfaces. La plus connue est le logiciel Xcas pour PC/Mac, mais Giac est aussi le moteur de calcul de la fenêtre de calcul formel de Geogebra. Xcas comme Geogebra regroupe en une seule interface plusieurs fonctionnalités : calcul formel, calcul numérique, géométrie dans le plan et l’espace, tableur ; Xcas met plus l’accent sur la programmation et la compatibilité Python (on peut programmer en Javascript dans Geogebra mais ce n’est pas aussi simple).

On peut aussi utiliser l’interface Xcas pour Firefox avec un navigateur compatible, donc depuis un PC/Mac, ou depuis une tablette ou un smartphone. Cette interface est moins complète (en particulier pas de tableur), mais permet d’échanger par un simple clic des sessions de travail (programme et historique de calculs) soit en privé par e-mail, soit en les publiant sur le forum de Xcas dans la section dédiée ou sur un autre forum. La personne qui reçoit une session de travail par mail clique sur le lien inclus, ce qui ouvre la session dans son navigateur, elle peut la modifier et renvoyer la session modifiée à l’expéditeur, on peut imaginer noter des compte-rendus de TP de cette manière. Enfin, il est possible d’exporter une session de travail Xcas pour l’importer sur une calculatrice Casio, plusieurs exemples de sessions sont disponibles sur cette page

Le portage de Xcas sur calculatrices s’appele χ\chicas. Historiquement, le premier portage de Xcas sur calculatrices a été fait pour les HP Prime (Giac en est le moteur de calcul formel), mais il s’agit d’un modèle haut de gamme (150 euros environ) très peu diffusé en France, puis sur TI Nspire pour proposer de calcul formel sur les modèles non CAS (dont le prix à l’époque était proche de 130 euros au lieu de 170). Ces calculatrices, de même que toutes les calculatrices proposant du calcul formel (TI nspire CX CAS, Casio Classpad), sont peu répandues dans le secondaire, en raison de leur prix dépassant la barre psychologique des 100 euros, elles sont essentiellement réservées aux élèves des milieux favorisés envisageant d’aller en prépas. Lorsque je fais un sondage dans mes amphis de licence le nombre d’étudiants ayant une calculatrice CAS se compte sur les doigts d’une main. C’est surement plus en classes prépas mais ca reste très minoritaire au lycée, on ne peut donc absolument pas accuser le calcul formel sur calculatrices d’être la cause des difficultés rencontrées par les étudiants en calcul littéral. Je pense que la vraie raison est la diminution du temps consacré à ces activités au lycée, en particulier en géométrie analytique, en raison de réductions de volumes horaire ou au profit d’autres thèmes, dont l’algorithmique.

Démocratiser un outil de vérification ou de calcul dans les cas techniques me parait donc important, et c’est la raison pour laquelle j’ai investi du temps de développement dans le portage de Xcas sur des calculatrices graphiques milieu de gamme, profitant du renouvellement de ces gammes par les constructeurs suite à l’introduction de Python :

À partir de cette rentrée, le nombre d’élèves ayant un modèle de calculatrices pouvant faire du calcul formel devrait significativement augmenter (d’ailleurs les modèles CAS de TI et Casio voient aussi leur prix diminuer)!
Notez que pour faire de l’algorithmique, χ\chicas est un environnement bien plus complet que le microPython proposé par les constructeurs de calculatrices, il offre un équivalent partiel des modules Python math+cmaths+numpy+scipy+matplotlib+giacpy+turtle, alors que le MicroPython des constructeurs se limite à maths, random, la tortue Python et un module graphique pixelisé pour Casio et TI, pour Numworks, s’y ajoute cmaths, tout cela étant complètement isolé du reste de la calculatrice. Ainsi une fonction microPython ne peut pas être représentée graphiquement dans l’application fonction, contrairement à une fonction χ\chicas qui peut être représentée graphiquement comme les fonctions usuelles par une simple commande plot.

5  Ressources

  

Retour à la page principale de Giac/Xcas.
Ce document a été traduit de LATEX par HEVEA