Exercices

1. (à rendre lors de la 1ère séance de ce TP)
   Écrire un programme MuPAD, maple ou xcas implémentant l'algorithme présenté en section 
2. (à rendre lors de la 1ère séance de ce TP)
   Il s'agit de résoudre $\cosh(x)/2=x$ sur $[0,1]$ en utilisant le théorème du point fixe, cf. la section . En utilisant un logiciel ou une calculatrice, donnez une valeur de $n$ pour laquelle $\vert u_{n+1}-u_n\vert\leq 10^{-3}$ et en déduire un encadrement de $x$.
3. (à rendre au début du 3ème TP)
   Résoudre $\cosh(x)=5x$ pour $x>0$ Indication: si la fonction de votre équation n'est pas contractante, cherchez une équation équivalente dont la fonction est contractante (indication: si $\vert f'\vert>1$ que peut-on dire de $\vert f^{-1}\,'\vert$ où $f^{-1}$ désigne la fonction réciproque de $f$?).
4. (à rendre lors de la 2ème séance de ce TP)
   Donner une valeur de $\sqrt{5}$ à $10^{-5}$ près en utilisant l'algorithme de Héron. Comparez avec l'itération de $f(x)=\frac{5x+5}{x+5}$. Justifiez dans les deux cas l'encadrement (on pourra utiliser une méthode analogue à celle du 2ème exercice)
5. (à rendre au début du 3ème TP)
   Rechercher par la méthode de Newton une racine de $x^3+x+1$.
6. (à rendre au début du 3ème TP)
   On suppose que la suite $u_n$ est donnée par la relation de récurrence :
   
   $$u_0=a ,\quad u_{n+1}=u_n^2+u_n-2$$
   
   
   On pose $f(x)=x^2+x-2$.
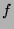   • Déterminer les points fixes $l_1$ et $l_2$ ($l_1<l_2$) de $f$ et calculer $f'$ en ces points.
     Faire le graphe de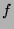 $f$ en précisant la tangente aux points fixes.
     Montrer que si $u_0>l_2$ la suite $(u_n)$ est croissante et divergente.
     Montrer que si $-\frac{9}{4}<u_0<l_2$ la suite $(u_n)$ est bornée.
     Montrer que quelque soit $u_0$ la suite $(u_n)$ n'est jamais convergente.
     Comment faites-vous pour savoir si $u_{2n}$ converge ? (détailler)
     
   • On suppose $-\frac{9}{4}<u_0<l_2$, montrer que $(u_n)$ posséde des suites extraites convergentes.
     On veut trouver les limites de ces suites extraites :
     Voici un programme MuPAD qui affiche pour chaque $u_0$ les valeurs de $u_{101}$ à $u_{200}$ (pour maple, remplacer end_for par od et return par RETURN)

     u:=proc(u0)
       local l;
       begin
         l:=[];
         for j from 1 to 100 do
           u0:=f(u0);
         end_for;
         for j from 1 to 100 do
           u0:=f(u0);
           l:=[op(l),u0];
         end_for;
       return (l);
     end_proc;
     

     Faire un programme qui affiche pour chaque $u_0$ les valeurs de $u_{2n}$ de $n=101$ à $n=200$ et faire un programme qui affiche pour chaque $u_0$ les valeurs de $u_{3n}$ de $n=101$ à $n=200$.
   • Chercher les points fixes de $fofof$ (en maple on peut utiliser fsolve et en MuPAD numeric::polyroots(p(x)); pour avoir les valeurs approchées des racines d'un polynôme p(x)).
     Essayer différentes valeurs de $u_0$ (par exemple $u_0=0$, $u_0=-2.25$,
     $u_0=0.8$, $u_0=0.801$, $u_0=0.802$ etc...). Qu'observez-vous ?
   • Montrer que si $0.802 \leq u_0 \leq 0.843$, $u_{3n}$ est convergente.
7. (facultatif)
   Reprendre en utilisant le procédé d'accélération de convergence d'Aitken la résolution de $\cosh(x)/2=x$ sur $[0,1]$ et de $\cosh(x)=5x$ pour $x>0$.
   Résoudre par ce procédé l'équation :
   $10\cos(x)=x$ sur $[0,\ 10]$
8. Suites extraites (facultatif)
   Écrire un programme donnant $k$ termes d'une sous-suite de la suite $u_n=\sin(n)$, dont tous les éléments sont dans l'intervalle $[0.98,1]$.