


Next: Méthode de Newton
Up: Complément de cours
Previous: Complément de cours
Théorème du point fixe
Soit 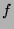 est une application continue de
est une application continue de 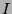 dans
dans 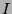 (
(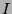 désigne un
intervalle fermé de
désigne un
intervalle fermé de 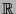 ).
Si
).
Si 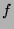 est contractante
(
est contractante
(
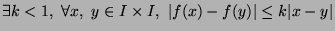 )
alors
)
alors 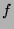 admet un point fixe
unique
admet un point fixe
unique 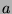 et la suite des itérées (
et la suite des itérées (
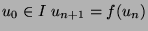 )
converge vers
)
converge vers 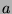 .
.
Exemples :
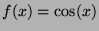 est contractante sur [0,1],
est contractante sur [0,1],
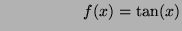 n'est pas contractante sur
n'est pas contractante sur
![$[\frac{\pi}{2},\ \frac{3\pi}{2}]$](img21.png)
Si 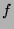 est contractante de rapport
est contractante de rapport 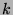 alors on a :
alors on a :
2003-02-19