Dualité tangent-cotangent.

  Par définition de df on a d_xf(v)=v(f) qui définit la dualité entre TM et T^*M. Graphiquement (cf. figure 3, p. ), on obtient la base duale de de la façon suivante: on construit le réseau de base , on prend les deux formes linéaires dont les lignes de niveau entières sont le réseau.

  
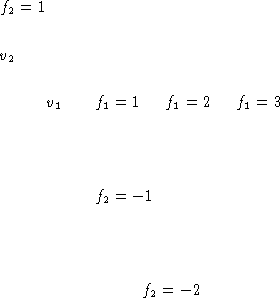
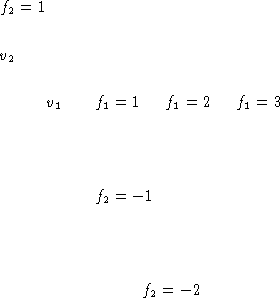
Figure: Une base de vecteurs et sa base duale.

En général, il n'y a pas d'isomorphisme canonique entre TX et T^*X. Il est nécessaire de disposer d'une donnée supplémentaire qui est une forme bilinéaire non dégénérée sur T_xX (par exemple une forme symétrique dans le cas des variétés riemanniennes ou une forme antisymétrique pour une variété symplectique).

On a vu que si , on peut définir . Par dualité, on peut définir : si , on pose

On vérifie que et sont bien duales l'une de l'autre: si ,

 

Mais il n'est pas possible de définir une application en général car si , on ne sait pas s'il admet un antécédent unique par . Lorsque est injective, on peut définir sur