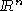. Pour
calculer une dérivée, il suffit de connaître la fonction
dans un voisinage du point considéré, donc on va demander à une
variété d'avoir une structure locale semblable à .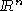
Par exemple, sur la figure 1, p. 
,
on observe que la courbe de gauche se recoupe en M donc ce n'est pas une
variété: en effet, on ne peut pas ramener un voisinage
du point double à un intervalle de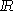 
. Par contre la courbe
de droite est une variété.
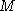
Figure: A gauche: ce n'est pas une variété,
à droite, c'est une variété.