La deuxième égalité est évidente, car 
commute avec
le produit tensoriel et le produit extérieur est un produit tensoriel
antisymétrisé.
La première propriété se montre en utilisant l'unicité de d. Il
suffit de voir que 
vérifie les propriétés du théorème 27.
Si f est une fonction 
, on a:
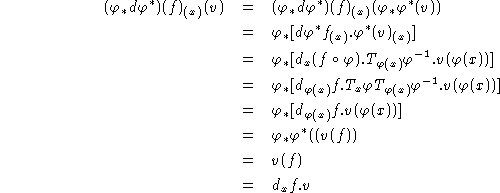
donc 
soit 
et:
De la proposition on déduit immédiatement le:
