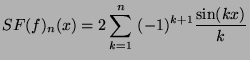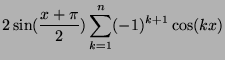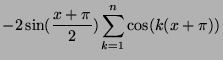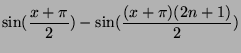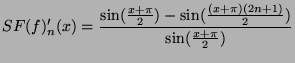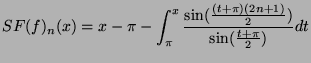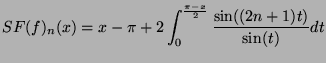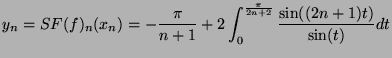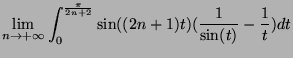suivant: Utilisation de la moyenne
monter: Les séries de Fourier
précédent: Rappels du cours
Les graphes des fonctions 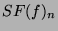 possède un maximum ayant comme
coordonnées
possède un maximum ayant comme
coordonnées 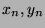 . Pour la fonction
. Pour la fonction 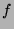 de l'exercice 6,
quand
de l'exercice 6,
quand 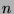 tend vers
tend vers 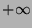 , on va montrer que :
Le calcul approché de
, on va montrer que :
Le calcul approché de 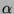 (cf exercice 3) montre que
(cf exercice 3) montre que
 .
Ces ''bosses'' au voisinage du point de discontinuité s'appellent le
phénomène de Gibbs.
.
Ces ''bosses'' au voisinage du point de discontinuité s'appellent le
phénomène de Gibbs.
Exercice 7 (à rendre au début du TP5)
Observation et démonstration de ce phénomène :
On cherche la limite de
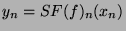 quand
quand 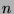 tend vers
tend vers 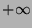
- de façon empirique
Déterminer les coordonnées 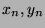 du maximum de :
du maximum de :
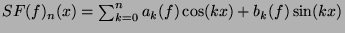 pour n=1, 2, 3, 4, 5, 6
pour n=1, 2, 3, 4, 5, 6
- de façon théorique
- Déterminer la valeur de
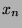
- Montrer que :
- Montrer que :
et en déduire que :
- En déduire que :
- En faisant un changement de variables montrer que :
- Prouver que :
- On définit la fonction
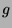 par :
Montrer que
par :
Montrer que 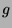 est continue, en déduire :
est continue, en déduire :
- Montrer que
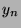 tend vers
tend vers
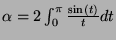 quand
quand 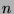 tend vers
tend vers 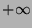 .
.



suivant: Utilisation de la moyenne
monter: Les séries de Fourier
précédent: Rappels du cours
2003-02-19
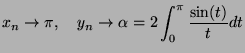
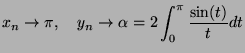
![]() quand
quand ![]() tend vers
tend vers ![]()