Les transformées de Laplace et de Laplace inverse

suivant: Les vecteurs et les monter: Aperçu des possibilités des précédent: Les équations différentielles

La transformée de Laplace d'une fonction F(x) est la fonction f définie par :

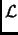
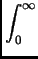f (s) = $\displaystyle \mathcal {L}$ (F)(s) = $\displaystyle \int_{0}^{\infty}$ e^-sxF(x)dx

On tape, pour avoir la transformée de Laplace de exp(ax) :

$\displaystyle \tt laplace(exp(a*x),x,s)$

On obtient pour s > a:

$\displaystyle \tt -1/(a-s)$

On tape, pour avoir la transformée de Laplace de x :

$\displaystyle \tt laplace(x,x,s)$

On obtient pour s > 0:

$\displaystyle \tt 1/s^2$

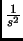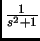On tape, pour avoir la transformée de Laplace inverse de ${\frac{1}{s^2}}$ + ${\frac{1}{s^2+1}}$ :

$\displaystyle \tt ilaplace(1/s^2+1/(s^2+1),s,x)$

On obtient :

$\displaystyle \tt x+sin(x)$

Documentation de giac écrite par Renée De Graeve