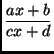suivant: À propos de ce
monter: miastp2_2003
précédent: Résoudre un système linéaire
On souhaite étudier des suites récurrentes (un) définies par
un + 1 = f (un) et u0, où f est une fonction de
 dans
dans
 (par exemple
f (x) =
(par exemple
f (x) = 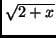 ).
).
Exercice 2 (à rendre à la fin de la 2ème séance de TP)
Écrire une fonction debut prenant en argument u0, la fonction f
et un entier n et renvoyant la liste
{u0, u1,..., un}.
Utilisez la fonction debut pour calculer les 50 premiers
termes de la suite
u0 = 0, un + 1 = 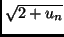 . Que constatez-vous
lorsque vous prenez
. Que constatez-vous
lorsque vous prenez u0:=0 et u0:=0.0 comme valeurs
initiales? Pourquoi cette différence? Quels sont les avantages
et inconvénients d'utiliser une valeur initiale exacte ou approchée?
Le programme précédent donne une idée de la convergence
de la suite, mais ne donne aucune information quantitative
sur la vitesse de convergence. Au lieu de renvoyer un nombre fixé
de termes de la suite, on va effectuer un test d'arrêt selon la
valeur
| un + 1 - un| comparé à un nombre positif (petit)
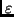 fixé à l'avance. Pour éviter que le programme boucle
indéfiniment lorsque la suite ne converge pas (ou converge
trop lentement pour la machine), on fixe aussi un nombre maximal
d'itération N.
fixé à l'avance. Pour éviter que le programme boucle
indéfiniment lorsque la suite ne converge pas (ou converge
trop lentement pour la machine), on fixe aussi un nombre maximal
d'itération N.
Exercice 3 (à rendre à la fin de la 2ème séance de TP)
Écrire une fonction iter prenant en argument
la fonction f, la valeur de
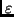 et de N
qui s'arrête si l'une des conditions est satisfaite :
| un + 1 - un| <
et de N
qui s'arrête si l'une des conditions est satisfaite :
| un + 1 - un| < 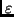 ou le nombre d'itérations dépasse N.
Dans le premier cas la fonction renverra la valeur de un + 1, dans
le second cas une séquence composée de uN et de N.
ou le nombre d'itérations dépasse N.
Dans le premier cas la fonction renverra la valeur de un + 1, dans
le second cas une séquence composée de uN et de N.
On suppose que la fonction f satisfait aux hypothèses du
théorème du point fixe (on notera k < 1 la constante de
ce théorème), déterminer en fonction de k et un + 1
un encadrement de la limite l de la suite un.
Exercice 4 (à rendre au début de la 3ème séance de TP)
Vérifier les hypothèses du théorème du point fixe
pour
f (x) = 3 cos(x/3) sur [0, 1]. Déterminer
une valeur approchée de la limite de un + 1
à 10-3 près en utilisant la fonction iter
précédente.
Déterminer une fraction rationnelle f à coefficients entiers
f (
x) =
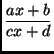
ayant comme point fixe 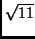 et un intervalle I contenant
et un intervalle I contenant
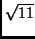 sur lequel
les hypothèses du théoréme du point fixe sont satisfaites.
En utilisant la fonction
sur lequel
les hypothèses du théoréme du point fixe sont satisfaites.
En utilisant la fonction iter, trouver un encadrement de
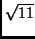 à 10-2 près par une fraction d'entiers. En
quoi ce type de suite récurrente est-il intéressant?
à 10-2 près par une fraction d'entiers. En
quoi ce type de suite récurrente est-il intéressant?



suivant: À propos de ce
monter: miastp2_2003
précédent: Résoudre un système linéaire
Bernard Parisse
2004-06-04