Espace tangent

  On va donner une définition abstraite de l'espace tangent à une variété en commençant par voir les vecteurs de comme des directions de dérivation de fonctions de ( de à valeurs dans ).

Soit une fonction dans un voisinage de et soit un vecteur, on leur associe la dérivée de f selon v en m:

en coordonnées locales:

On peut voir l'action de v comme étant une fonctionnelle (que l'on note encore v) de f, qui vérifie les propriétés de linéarité et de Leibniz:

 

 

Réciproquement, si une fonctionnelle vérifie les propriétés (1) et (2), alors montrons que est identique à l'action d'un vecteur v.

On observe d'abord que donc puis par linéarité . Soit maintenant une fonction dans un voisinage de , posons pour :

La fonction g est sur [0,1], donc

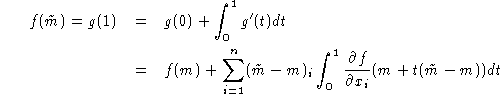
Donc, par linéarité et en appliquant Leibniz:

Finalement:

où v a pour coordonnées dans la base canonique.

Notation:
On note le i-ième vecteur de la base canonique. Ce qui se justifie par le fait que

Revenons maintenant au cas d'une variété quelconque. On note l'ensemble des fonctions qui sont sur un voisinage de m.

 

 

Preuve:
On définit la structure d'espace vectoriel sur T_mM par la somme de fonctionnelles et le produit d'une fonctionnelle par un scalaire. Considérons un ouvert O de M contenant m, source de la carte locale x à valeur dans l'ouvert U de . A tout couple (m,v) de TM, on associe:

On observe tout d'abord que x_* est un automorphisme entre T_mM et l'espace vectoriel (en utilisant l'identification des vecteurs de avec les fonctionnelles vérifiant (1) et (2)). Donc . A la carte x est associée canoniquement une base de T_mM dont le i-ième vecteur est . Lorsqu'il n'y a pas de confusion possible, on note encore cette base . Ceci est justifié par le fait que pour les fonctions la valeur de v(x_i) est . D'ailleurs on peut voir Tx en coordonnées par:

On considère maintenant deux cartes locales x et y, montrons que Tx et Ty sont compatibles. On se donne donc dans l'image de Tx et on calcule . Notons , donc m=x^-1(x_m) et:

Comme M est une variété, il est clair que est en x_m. Il reste à exprimer les en fonction des . Pour voisin de m d'image par la carte locale x, on a:

Donc:

Finalement est une combinaison linéaire à coefficients des , la matrice de l'application linéaire qui permet de passer du vecteur au vecteur est la matrice:

 

qui est inversible car est un difféomorphisme .

Si v a pour coordonnées dans la base et dans la base , et sont reliés par la formule (3) donc en faisant (i.e. pour ), on obtient:

 

 

Soit M une sous-variété de N. Alors TM est canoniquement une sous-variété de TN, en effet si , on peut le voir comme un vecteur de T_mN en définissant son action sur par restriction: v(f_|M). Si x est une carte locale de N dans laquelle M a pour équation x₁=...=x_k=0 alors Tx est une carte locale de TN dans laquelle TM a pour équations x₁=...=x_k=v₁=...=v_k=0 où (v_k) désigne les coordonnées de v dans la base .

Exemples:
Considérons S² et un point situé dans la source de la carte locale:

Soit v un vecteur de , alors si donc si:

où (v_x,v_y,v_z) désignent les coordonnées de v dans la base canonique . Finalement si:

que l'on peut réécrire sous la forme:

où f(x,y,z)=x²+y²+z² est la fonction de rang constant au voisinage de S², telle que S²=f^-1(1).

Ce fait est d'ailleurs général, si f est une application comme au théorème 7, et si alors (cf. [4, (16.8.8), p.42,]).

Les groupes classiques de matrices (inversibles, orthogonales, unitaires) ont des structures de variété, ce sont d'ailleurs des sous-variétés de . Les espaces tangents en l'identité sont alors respectivement toutes les matrices, les matrices antisymétriques et les matrices antihermitiennes. La structure de groupe permet d'identifier les espaces tangents en d'autres matrices avec ces espaces vectoriels de matrices.

 

 

La linéarité est évidente et le caractère se montre en coordonnées locales.

Exemple:
L'application f_A définie sur par f_A(G)=G^-1AG admet pour application tangente en G: