Produit intérieur par un champ de vecteurs.

 

 

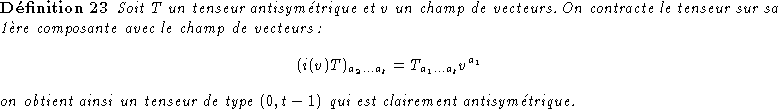
Exemple:
Si v a pour coordonnées (v₁,v₂) dans la base duale de la base (dx¹,dx²,...) alors:

  

 

Preuve:

 

On décompose alors la somme en regardant si ou à . Dans le premier cas, l'indice a₁ est dans le tenseur T et dans le deuxième cas dans le tenseur R.

Premier cas:
Si , on associe à la permutation en posant

(si k=1, on pose ), on peut réécrire sous la forme:

Si , on a , donc

car T est antisymétrique. Si k=1, l'égalité entre les deux extrêmes est évidente. Donc la première partie de la somme (11) s'écrit:

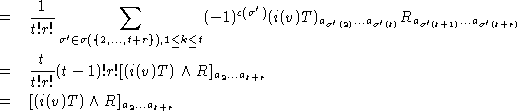
Deuxième cas:
On associe à comme dans le premier cas, et on obtient comme terme général de la somme:

On fait alors le changement d'indice de sommation:

le terme général s'écrit alors:

On utilise enfin l'antisymétrie du tenseur R, la deuxième partie de la somme s'écrit:

qui est bien égal à .