


Next: Programmation.
Up: Correction d'erreurs de transmission:
Previous: La parité.
La PCE.
La méthode précédente permet de savoir avec certitude qu'une
transmission s'est mal passée si la parité n'est pas respectée,
mais elle ne permet pas de corriger une erreur. La méthode décrite
dans cette section permet de corriger une erreur (en faisant
l'hypothèse que la transmission a engendré au plus 2 erreurs).
Cette fois-ci on regroupe l'information à transmettre par paquets de 15
octets (de parité paire) et on ajoute un 16ème octet (dont on
ajuste aussi la parité). On va maintenant expliquer comment on
calcule ce 16ème octet en fonction des 15 précédents.
Soit
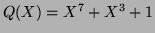 . Étant donnés 15 octets
. Étant donnés 15 octets 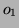 , ...,
, ..., 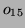 de parité paire, on calcule le polynôme:
de parité paire, on calcule le polynôme:
(le terme de plus bas degré est donc de degré au moins 7:
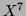 obtenu pour
obtenu pour 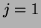 ).
).
On calcule ensuite le reste de la division euclidienne de 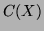 par
par 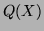 ce qui donne un polynôme
ce qui donne un polynôme 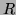 de degré 6, l'octet
de degré 6, l'octet 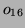 est alors
l'octet correspondant à
est alors
l'octet correspondant à 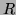 (plus précisément tel que
(plus précisément tel que
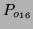 coinncide avec
coinncide avec 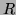 sauf pour le terme de degré
7).
sauf pour le terme de degré
7).
A l'autre extrémité, le récepteur reçoit 16 octets
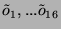 et forme le polynôme
et forme le polynôme
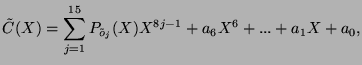
où
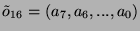
Si la transmission s'est bien passée,
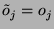 donc
donc
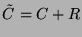 est divisible par
est divisible par 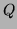 (car
(car  dans
dans
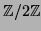 ).
Réciproquement, si tous les octets
).
Réciproquement, si tous les octets
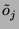 sont de parité
paire et si
sont de parité
paire et si 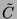 est divisible par
est divisible par 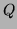 alors soit la transmission
s'est bien passée soit le nombre d'erreurs est supérieur ou égal à 2.
alors soit la transmission
s'est bien passée soit le nombre d'erreurs est supérieur ou égal à 2.
S'il y a une erreur de transmission et une seule, alors il exixste
un entier
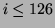 tel que:
tel que:
que détermine à l'aide du reste de la division euclidienne
de 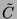 par
par 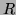 et de la parité des
et de la parité des
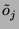 .
.
Programmez un algorithme mettant en oeuvre cette procédure et
testez la en créant des erreurs de manière aléatoire.



Next: Programmation.
Up: Correction d'erreurs de transmission:
Previous: La parité.
2001-01-19
![]() . Étant donnés 15 octets
. Étant donnés 15 octets ![]() , ...,
, ..., ![]() de parité paire, on calcule le polynôme:
de parité paire, on calcule le polynôme:
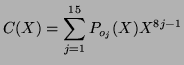
![]() et forme le polynôme
et forme le polynôme
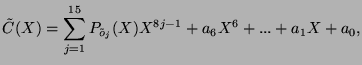 où
où ![]() tel que:
tel que: