


Next: Références
Up: Construction BKW pour l'opérateur
Previous: Application à un potentiel
Nous améliorons ici le résultat du deuxième auteur (cf.
[4]) sur le découplage des valeurs propres par un
effet de type Aharonov-Bohm, sans faire d'hypothèse de type
non relativiste. Il s'agit de l'analogue dans le cas de l'opérateur
de Dirac du travail de B.Helffer ([1]) pour l'opérateur
de Schrödinger.
Rappelons brièvement le problème considéré:
on considère un opérateur de Dirac avec potentiel électrique
et champ magnétique ayant les propriétés suivantes:
- le champ électrique possède un puits de potentiel en un point
P, on s'intéresse au spectre de l'opérateur de Dirac pour
des valeurs de l'énergie correspondant àu puits P,
- le champ magnétique est nul sauf dans un cylindre. On suppose
que le cylindre est situé dans unz zone classiquement interdite, à
une distance d'Agmon S' de P,
- il existe un unique lacet contenant P et encerclant le cylindre
de longueur d'Agmon S minimale parmi les lacets contournant la
zone magnétisée,
- S<2S'. C'est-à-dire que si on modifie le potentiel dans
le cylindre l'effet sur les valeurs propres est négligeable devant
e-S/h .
On s'aperçoit alors que l'effet du champ magnétique, bien que
confiné dans le cylindre, est de l'ordre de e-S/h, plus précisément
une valeur propre double 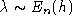 en l'absence de champ magnétique
se transforme en deux valeurs propres
en l'absence de champ magnétique
se transforme en deux valeurs propres 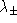 reliées à
reliées à
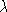 (sous certaines hypothèses de non-dégénérescence
du lacet minimal, hypothèses qui sont précisées dans [4])
par:
(sous certaines hypothèses de non-dégénérescence
du lacet minimal, hypothèses qui sont précisées dans [4])
par:
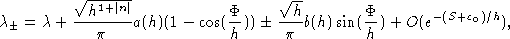
où a(h) et b(h) sont des symboles semi-classiques et 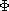 est
le flux du champ à travers le lacet.
On montre que les symboles principaux de a(h) et de b(h)
sont proportionnels respectivement à la partie réelle et imaginaires
de la valeur propre de
l'isomorphisme du lacet contournant la zone magnétisée pris
au point situé à mi-distance d'Agmon sur ce lacet. On peut
donc les calculer à l'aide du théorème (6) lorsque
le lacet minimal reste dans un plan, et cela sans supposer comme
dans [4, Théorème 2,] que l'on est en limite non
relativiste. De plus le théorème 7 permet
d'affirmer qu'il existe de nombreux exemples de potentiels pour
lesquels les valeurs propres
est
le flux du champ à travers le lacet.
On montre que les symboles principaux de a(h) et de b(h)
sont proportionnels respectivement à la partie réelle et imaginaires
de la valeur propre de
l'isomorphisme du lacet contournant la zone magnétisée pris
au point situé à mi-distance d'Agmon sur ce lacet. On peut
donc les calculer à l'aide du théorème (6) lorsque
le lacet minimal reste dans un plan, et cela sans supposer comme
dans [4, Théorème 2,] que l'on est en limite non
relativiste. De plus le théorème 7 permet
d'affirmer qu'il existe de nombreux exemples de potentiels pour
lesquels les valeurs propres 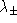 sont distinctes,
puisque leur différence est proportionnelle à
sont distinctes,
puisque leur différence est proportionnelle à 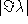 .
.
Remerciements.
Le second auteur tient à remercier Luc Rozoy pour les éclaircissements
qu'il lui a apporté en géométrie, lui permettant d'aboutir
au théorème 7. Ces deux
théorèmes suffisent à prouver la non-nullité générique
du découplage entre valeurs propres des sections 5
et 6, mais nous n'avons pas su répondre à une question
plus ambitieuse:
Existe-t-il des potentiels périodiques dont la géodésique d'Agmon
reliant les
puits les plus proches soit convexe (i.e. de courbure de signe constant)?



Next: Références
Up: Construction BKW pour l'opérateur
Previous: Application à un potentiel
Bernard Parisse
Tue Mar 25 14:27:08 MET 1997
![]()
![]() est
le flux du champ à travers le lacet.
On montre que les symboles principaux de a(h) et de b(h)
sont proportionnels respectivement à la partie réelle et imaginaires
de la valeur propre de
l'isomorphisme du lacet contournant la zone magnétisée pris
au point situé à mi-distance d'Agmon sur ce lacet. On peut
donc les calculer à l'aide du théorème (6) lorsque
le lacet minimal reste dans un plan, et cela sans supposer comme
dans [4, Théorème 2,] que l'on est en limite non
relativiste. De plus le théorème 7 permet
d'affirmer qu'il existe de nombreux exemples de potentiels pour
lesquels les valeurs propres
est
le flux du champ à travers le lacet.
On montre que les symboles principaux de a(h) et de b(h)
sont proportionnels respectivement à la partie réelle et imaginaires
de la valeur propre de
l'isomorphisme du lacet contournant la zone magnétisée pris
au point situé à mi-distance d'Agmon sur ce lacet. On peut
donc les calculer à l'aide du théorème (6) lorsque
le lacet minimal reste dans un plan, et cela sans supposer comme
dans [4, Théorème 2,] que l'on est en limite non
relativiste. De plus le théorème 7 permet
d'affirmer qu'il existe de nombreux exemples de potentiels pour
lesquels les valeurs propres ![]() sont distinctes,
puisque leur différence est proportionnelle à
sont distinctes,
puisque leur différence est proportionnelle à ![]() .
.