Chapitre 9  Le "baccalauréat" suisse de 1896

Il s’agit des épreuves que Einstein passe en 1896 à l’age de 17 ans et demi en Suisse, ce qui est l’équivalent de notre baccalauréat.
À l’époque tous les calculs étaient lons et fastidieux car faits à l’aide de table

9.1  Épreuve de géométrie de 4h

9.1.1  Exercice 1

L’énoncé

Un triangle inscrit dans un cercle de rayon R=10 a ses hauteurs proportionnelles à 2, 3 et 4.
Calculer les angles et un côté.

La solution avec Xcas

Par hypothèse, il existe k∈ ℝ⁺ tel que :
h_A=2k, h_B=3k, h_C=4k,
On a :
sin(A)=h_B/c=h_C/b=3k/c=4k/b
sin(B)=h_A/c=h_C/a=2k/c=4k/a
sin(C)=h_B/a=h_A/b=3k/a=2k/b
Donc :
a=2c et b=4c/3 et
a²=c²+b²−2bccos(A)
b²=a²+c²−2accos(B)
c²=a²+b²−2abcos(C)
On fait une figure :

Donc on a:

• 4c4c/3cos(C)=c²(4+16/9−1=c²43/9soit :
  cos(C)=43/16*3=43/48 et sin(C)=√455/48
  On tape :
  C:=acos(43/48.)
  On obtient :
  0.460493425059
  
• 4c²cos(B)=4c²+c²−16c²/9=c²29/9 soit :
  cos(B)=29/36 et sin(B)=√455/36
  On tape :
  B:=acos(29/36.)
  On obtient :
  0.634183840824
  
• 2c4c/3cos(A)=+c²+16c²/9−4c²=c²−11/9soit :
  cos(A)=−11/24 et sin(A)=√455/24
  On tape :
  A:=acos(-11/24.)
  On obtient :
  2.04691538771
  

On sait que :
a/sin(A)=b/sin(B)=c/sin(C)=2R=20 et
Donc on a :

• c=20sin(C)=5√455/12
  On tape :
  c:=5*sqrt(455)/12.)
  On obtient :
  8.88780375321
  
• b=4c/3=5√455/9
  On tape :
  b:=4c/3
  On obtient :
  11.8504050043
  
• a=2c=5√455/6
  On tape :
  a:=2*c)
  On obtient :
  17.7756075064
  

On construit le triangle ABC et on tape :

B:=point(0);
C:=point(5*sqrt(455)/6);
A:=point(5*sqrt(455)/12*(29/36+i*sqrt(455)/36));
triangle(A,B,C);
cc:=circonscrit(A,B,C);

0n tape :
normal(rayon(cc));
On obtient : 10
0n tape :
A1:=projection(droite(B,C),A);
normal(longueur(A,A1));
On obtient : 2275/432
Donc le coefficient de proportionnalité k pour les hauteurs vaut :
2275/864

Une autre solution avec Xcas

Si S est l’aire du triangle ABC on a :
2S=ah_A=bh_B=ch_c
Par hypothèse, il existe k∈ ℝ⁺ tel que :
h_A=2k, h_B=3k, h_C=4k donc,
2a=3b=4c c’està dire a=2c et b=4/3c
Le triangle ABC est donc semblable au triangle de côtés :
a=6, b=4, c=3
On sait que le rayon R du cercle circonscrit est égal à :
R=abc/4√p(p−a)(p−b)(p−c) avec 2p=a+b+c.
Avec Xcas, on calcul le rayon du cercle circonscrit au triangle a=6, b=4, c=3, on tape :
a:=6
b:=4
c:=3
p:=(a+b+c)/2
R:=a*b*c/4/sqrt(p*(p-a)*(p-b)*(p-c))
On obtient :
(72*sqrt(455))/455
On veut avoir que le rayon du cercle circonscrit soit ègale à 10 donc le triangle cherché est proportionnel au triangle de côtés a=6, b=4, c=3 avec comme coefficient de proportionnalité :
k= 10√455/72=5√455/36.
Les côtés du triangle cherché sont donc :
BC= 5 √455/6, AC= 5 √455/9, AB= 5 √455/12
Les angles de ABC sont les mêmes que les angles du triangle de côtés a=6, b=4, c=3 donc on a :
2bccos(A)=b²+c²−a²
2accos(B)=a²+c²−b²
2abcos(C)=a²+b²−c²
Avec Xcas, on tape :
A:=evalf(acos((b^2+c^2-a^2)/(2*b*c)))
On obtient :
2.04691538771
On tape :
B:=evalf(acos((a^2+c^2-b^2)/(2*a*c)))
On obtient :
0.634183840824
On tape :
C:=evalf(acos((a^2+b^2-c^2)/(2*a*b)))
On obtient :
0.460493425059

La solution de Xcas

Xcas fait de la géométrie analytique.
On dessine le triangle direct ABC de côtés a=6, b=4, c=3 en mettant B à l’origine du repère et C sur l’axe des x.
On tape :

B:=point(0);
C:=point(6);
A:=inter(cercle(0,3),cercle(5,4))[1];
triangle(A,B,C,affichage=1+epaisseur_ligne_2);
tA:=angle(A,B,C);
tB:=angle(B,C,A);
tC:=angle(C,A,B);
cc:=circonscrit(A,B,C);
R:=rayon(cc);

On obtient :

Avec :
pour tA : atan(((sqrt(455))/2)/(-11/2))+(2*pi)/2
pour tB :atan(((sqrt(455))/2)/(29/2))
pour tC : -(atan(((sqrt(455))/2)/(43/2)))
pour evalf(tA) : 2.04691538771
pour evalf(tB) : 0.634183840824
pour evalf(tC) : 0.460493425059
pour R : (72*sqrt(455))/455

9.1.2  Exercice 2

L’énoncé

On donne un cercle de rayon r dont le centre se trouve à l’origine O d’un repère orthonormal.
On considère les cordes de ce cercle perpendiculaires à l’axe des x.
Les cercles ayant ces cordes comme diamètres sont tangents à l’ellipse de demi-axes r√2 et r, aussi longtemps que la distance d de leur centre à O ne dépasse pas une certaine valeur maximale.
Démontrer cette proposition et déterminer la valeur maximale de d.

La solution avec Xcas

On considère la corde du cercle centre O et de rayon r qui a pour abscisse −r≤ a≤ r et qui est perpendiculaire à l’axe des x.
Le cercle de diamètre cette corde a donc pour rayon √r²−a² et pour équation :
(x−a)²+y²=r²−a² ou encore :
x²+y²−2ax+2a²−r²=0 Avec Xcas, on suppose que r=1 et on tape :

ellipse(-1,1,sqrt(2),affichage 
=1)supposons(a=[0.5,-1/sqrt(2),1/sqrt(2),0.1]);
C:=cerle(a,sqrt(1-a^2));

Puis, on fait bouger a en gardant la trace de C (menu M->Trace objet->C).
On obtient :

Nous allons montrer que l’enveloppe de ces cercles est une ellipse de centre O et de demi-axes r√2 et r (c’est ce que l’on voit sur la figure ci-dessus).
Le point M=(x,y) de contact du cercle et de son enveloppe vérifie les équations :
x²+y²−2ax+2a²−r²=0 et
−2x+4a=0 (obtenu en dérivant par rapport à a)
donc M=(2a,√r²−2*a²) ou M=(2a,−√r²−2*a²).
Il faut donc que r²−2*a²≥ 0 soit a≤ r√2/2.
Puisque a=x/2 M est sur la courbe d’équation :
x²+y²−2(x/2)x+2(x/2)²−r²=x²+y²−x²+x²/2−r²=x²+2y²−2r²0.
Donc M se déplace donc sur l’ellipse d’équation :
x²+2y²=2r².
Cette ellipse a pour centre O et pour demi-axes r√2 et r.

9.2  Épreuve d’algébre de 2h

9.2.1  L’énoncé

Dans un triangle on connait les distance l, m, n du centre du cercle inscrit aux sommets.
Déterminer le rayon r du cercle inscrit lorsque l=1, m=1/2, n=1/3

La solution avec Xcas

Soient le triangle ABC et I le centre de son cercle inscrit.
On pose IA=l, IB=m et IC=n.

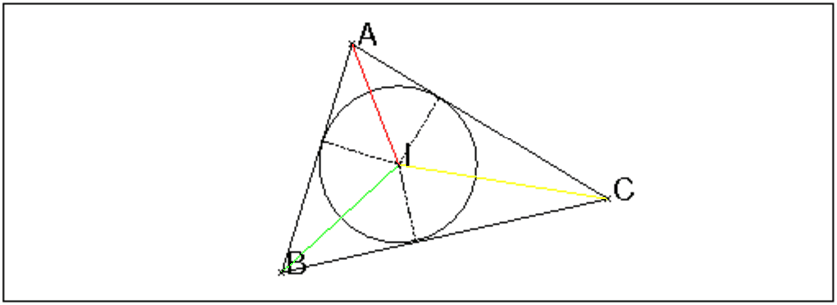
On a :
sin(A/2)=r/l=r,   sin(B/2)=r/m=2r,   sin(C/2)=r/n=3r
On sait que A + B + C =π donc
sin(C/2)=sin(π/2−A+B/2)=cos(A+B/2).
On sait que :
A /2<π/2 donc cos(A/2)=√1−r²
B /2<π/2 donc cos(B/2)=√1−4r²
Donc :
sin(C/2)=√1−r²√1−4r²−2r²=3r r vérifie donc l’équation :
√(1−r²)(1−4r²)=3r+2r² c’est à dire
(3r+2r²)²−(1−r²)(1−4r²)=0
On tape :
normal((3r+2r^2)^2)-(1-r^2)*(1-4r^2)
On obtient : 12*r^3+14*r^2-1
On tape :
fsolve( 12*r^3+14*r^2-1,r)
On obtient :
[0.243126179572,-0.312313414531,-1.09747943171]
r est positif donc r=0.243126179572.

Si on veut faire le calcul en utilisant la méthode de Newton.
On tape :
g1:=function_diff(g)
g1(x)
On obtient comme dérivé de g(x) :
36*x^2+28*x
Donc la fonction g est croissante sur ℝ⁺
On tape :
g(x):=12x^3+14x^2-1
plotfunc(g(x),x=-1.5..1)
On obtient :

On a :

• la fonction g est croissante et continue sur ℝ⁺,
• g(0)=−1,
• g(1/2)=4

donc d’après le théorème des valeurs intermédiaires g a un seul zéro r sur ℝ⁺ qui est compris entre 0 et 1/2.
La valeur de r est proche de 1/5=0.2 (c’est l’intersection du segment AB (A=(0,−1), B=1/2,4) avec l’axe des x) On peut chercher la solution r de 12x³+14x²−1=0 pour x>0 avec la méthode de Newton.
On tape :
h(x):=x-g(x)/g1(x)
b:=h(0.2)
On obtient :
0.248863636364
On tape :
b:=h(b)
On obtient :
0.243208102696
On tape :
b:=h(b)
On obtient :
0.243126196656
On tape :
b:=h(b)
On obtient :
0.243126179572
Donc la méthode de Newton donne après 4 itérations :
r=0.243126179572
Remarque
Einstein résout l’équation : 12x³+14x²−1=0 on posant X=A/x et en utilisant les formules de Cardan pour résoudre : X³−14X−12=0.