


suivant: Phénomène de Gibbs
monter: Les séries de Fourier
précédent: Logiciels
On sait que les coefficients de Fourier d'une fonction, 2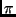 -périodique et
intégrable sur tout intervalle fermé borné, sont définis pour
n
-périodique et
intégrable sur tout intervalle fermé borné, sont définis pour
n 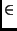
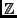 et pour
et pour
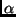
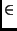
 par :
par :
cn(
f )=
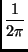
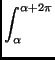 f
f (
t)
e-intdt
et que la série de Fourier associée à f est :
SF(
f )(
x) =
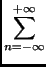 cn
cn(
f )
einx
On peut aussi définir les coefficients de Fourier réels pour
n 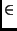
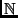 et pour
et pour
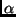
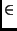
 par :
par :
| an(f ) |
= |
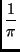 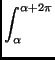 f (t)cos(nt)dt f (t)cos(nt)dt |
|
| bn(f ) |
= |
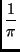 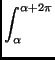 f (t)sin(nt)dt f (t)sin(nt)dt |
|
On a alors :
SF(
f )(
x) =
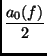
+
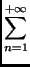
(
an(
f )cos(
nx) +
bn(
f )sin(
nx))
Théorème de Dirichlet
Si au point x0, f admet une limite à droite et une limite à gauche
(que l'on note
f (x0 + 0) et f (x0 - 0)), ainsi qu' une dérivée à droite et une
dérivée à gauche, alors la série
SF(f )(x0) converge vers
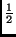 (f (x0 - 0) + f (x0 + 0)).
(f (x0 - 0) + f (x0 + 0)).
En particulier si f est dérivable pour tout x, SF(f )(x) converge vers
f (x).
Exercice 1 (à rendre à la fin de la séance)
Trouver le développement
SF(
f )(
x) =
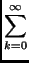 ak
ak(
f )cos(
kx) +
bk(
f )sin(
kx)
en séries de Fourier de la fonction f
périodique de période 2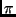 définie par :
définie par :
f (
x) =
x pour exp(
x/2)
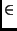
] -
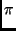
;
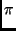
].
On note :
SF(
f )
n(
x) =
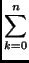 ak
ak(
f )cos(
kx) +
bk(
f )sin(
kx)
Donner la valeur et tracer sur un même graphique et pour
x 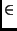 [- 4;4]
les graphes des fonctions suivantes :
[- 4;4]
les graphes des fonctions suivantes :
f (x), SF(f )1(x), SF(f )2(x), SF(f )3(x), SF(f )4(x), SF(f )5(x), SF(f )6(x)



suivant: Phénomène de Gibbs
monter: Les séries de Fourier
précédent: Logiciels
Bernard Parisse
2004-06-04
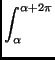 f (t)e-intdt
f (t)e-intdt
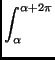 f (t)e-intdt
f (t)e-intdt
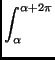 f (t)cos(nt)dt
f (t)cos(nt)dt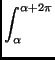 f (t)sin(nt)dt
f (t)sin(nt)dt