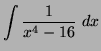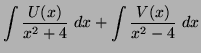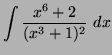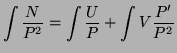suivant: Valeur d'un polynôme en
monter: miastp1
précédent: miastp1
Arithmétique des polynômes.
Comme pour les entiers, on peut faire la division euclidienne de deux
polynômes 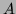 et
et 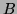 de degrés
de degrés 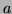 et
et 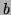 , on obtient le quotient
, on obtient le quotient
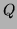 de degré
de degré 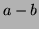 (si
(si 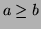 ) et le reste
) et le reste 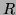 de degré
strictement inférieur à
de degré
strictement inférieur à 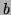 vérifiant l'égalité :
vérifiant l'égalité :
L'algorithme d'Euclide permet de calculer le PGCD de deux polynômes
exactement comme pour calculer le PGCD de deux entiers.
Algorithme de Bézout (dit aussi PGCD étendu): lorsque
deux polynômes 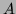 et
et 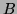 ont comme PGCD le polynôme
ont comme PGCD le polynôme 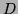 ,
il existe deux polynômes
,
il existe deux polynômes 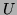 et
et 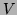 tels que :
tels que :
Exercice 1 (à rendre à la fin de la 1ère séance de TP) :
Application à la recherche de racines multiples.
Rappel : Si 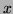 est une racine de mulitplicité
est une racine de mulitplicité 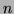 de
de 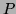 , alors
, alors
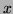 est une racine de multiplicté
est une racine de multiplicté 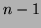 de
de 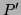 ,
, 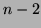 de
de 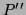 ,
etc. En particulier si
,
etc. En particulier si 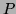 et
et 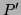 sont premiers entre eux,
toutes les racines de
sont premiers entre eux,
toutes les racines de 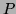 sont de multiplicité 1.
sont de multiplicité 1.
On considère le polynôme
Calculer avec un logiciel de calcul formel 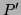 et
et 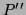 , le PGCD de
, le PGCD de 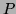 et
et
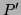 et le PGCD de
et le PGCD de 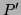 et
et 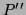 . En déduire que
. En déduire que 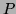 admet un facteur
de multiplicité 3 et un facteur de multiplicité 2.
admet un facteur
de multiplicité 3 et un facteur de multiplicité 2.
Exercice 2 (à rendre à la fin de la 1ère séance de TP) :
Application au calcul de l'intégrale :
On factorise le dénominateur de la fraction sous la forme
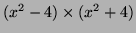 . Déterminer avec un logiciel de calcul
formel deux polynômes
. Déterminer avec un logiciel de calcul
formel deux polynômes 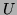 et
et 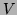 tels que :
tels que :
en déduire que l'intégrale de départ vaut :
calculer ces intégrales en expliquant quels calculs intermédiaires
vous avez effectués avec le logiciel.
Exercice 3 (à rendre au début de la 3ème séance de TP) :
Application au calcul de l'intégrale
Effectuer la division euclidienne du numérateur par le dénominateur
pour se ramener à l'intégrale d'une fraction dont le
numérateur 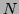 est de degré inférieur au dénominateur.
Soit
est de degré inférieur au dénominateur.
Soit 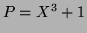 , calculer
, calculer 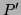 et le PGCD de
et le PGCD de 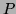 et
et 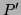 , en déduire
qu'il existe des polynômes
, en déduire
qu'il existe des polynômes 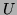 et
et 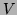 tels que:
calculer ces deux polynômes avec un logiciel.
On décompose alors l'intégrale en deux morceaux :
tels que:
calculer ces deux polynômes avec un logiciel.
On décompose alors l'intégrale en deux morceaux :
Faites une intégration par parties sur le deuxième terme
et en déduire la valeur de l'intégrale du départ.



suivant: Valeur d'un polynôme en
monter: miastp1
précédent: miastp1
2003-02-19
![]() et
et ![]() ont comme PGCD le polynôme
ont comme PGCD le polynôme ![]() ,
il existe deux polynômes
,
il existe deux polynômes ![]() et
et ![]() tels que :
tels que :
![]() est une racine de mulitplicité
est une racine de mulitplicité ![]() de
de ![]() , alors
, alors
![]() est une racine de multiplicté
est une racine de multiplicté ![]() de
de ![]() ,
, ![]() de
de ![]() ,
etc. En particulier si
,
etc. En particulier si ![]() et
et ![]() sont premiers entre eux,
toutes les racines de
sont premiers entre eux,
toutes les racines de ![]() sont de multiplicité 1.
sont de multiplicité 1.