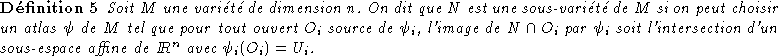
Exemples:
![]()
la fonction:
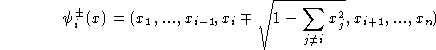
et sur ![]() on prend la carte identité. On
recouvre bien
on prend la carte identité. On
recouvre bien ![]() et l'image par
et l'image par ![]() de
de ![]() est:
est:
![]()
Si on se donne deux variétés M et M' de dimensions m et m',
le produit cartésien ![]() est encore une variété de dimension
m+m'.
est encore une variété de dimension
m+m'.
On peut ainsi construire de nombreux exemples de variétés. Un
énoncé permet de justifier la structure ![]() de variétés de base:
de variétés de base:
Par exemple, le cercle est une sous-variété de ![]() comme
image réciproque de 1 par:
comme
image réciproque de 1 par:
![]()
Par contre, le dessin à gauche de la figure 1 n'est pas une ligne de niveau d'une fonction de rang constant car df=0 au point double.
Un théorème dû à Whitney affirme en outre que toute variété
de dimension n peut être vue comme une sous-variété de
![]() .
.