


suivant: Les variables et les
monter: Aperçu des possibilités des
précédent: Aperçu des possibilités des
On tape :
On obtient :
On tape :
On obtient :
On tape pour factoriser 50! :
On obtient :
On tape :
On obtient :
On tape pour avoir une valeur approchée de 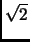 (par défaut on a
12 chiffres significatifs) :
On obtient pour avoir 22 chiffres significatifs :
On tape :
On tape :
On obtient :
On tape :
On obtient :
On tape :
On obtient :
(par défaut on a
12 chiffres significatifs) :
On obtient pour avoir 22 chiffres significatifs :
On tape :
On tape :
On obtient :
On tape :
On obtient :
On tape :
On obtient :
Documentation de giac écrite par Renée De Graeve