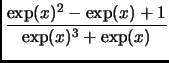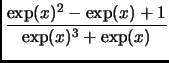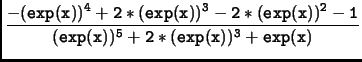On considère la fonction f de 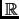 dans
dans 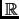 définie par :
définie par :
f (
x) =
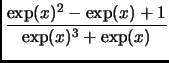
a) Montrer que pour tout
x 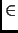
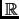 ,
P(x) = x4 - 2x3 + 2x2 + 1
,
P(x) = x4 - 2x3 + 2x2 + 1 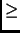 1
1
b) Étudier les variations de f et tracer son graphe.
c) Trouver l'équation de la tangente au graphe au point d'abscisse x = 0
d) Calculer
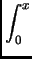 f (t)dt puis,
f (t)dt puis,
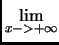
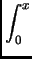 f (t)dt
f (t)dt
Réponses
a)
On tape :
On obtient :
On tape :
On obtient :
Donc pour tout
x 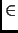
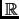 ,
x4 - 2x3 + 2x2
,
x4 - 2x3 + 2x2 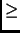 0
0
donc pour tout
x 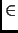
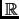 ,
P(x) = x4 - 2x3 + 2x2 + 1
,
P(x) = x4 - 2x3 + 2x2 + 1 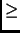 1
1
b)
On tape :
On obtient :
Le numérateur est négatif car il est égal à
- P(exp(x)) et le
dénominateur est strictement positif car il est égal à une somme de
termes strictement positifs. La fonction f est donc décroissante.
Cherchons la limite de f en + 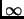 .
.
On tape :
On obtient :
Cherchons la limite de f en - 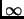 .
.
On tape :
On obtient :
On tape :
On obtient le graphe de f.
c)
On définit la fonction f, on tape :
On calcule f (0), on tape :
On obtient
On définit la fonction df comme étant la dérivée de f, on tape :
On calcule df (0), on tape :
On obtient :
L'équation de la tangente au point d'abscisse 0 est donc :
y = df (0)*x + f (0)
c'est à dire
y = - 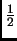 x +
x + 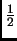 .
ou encore on tape :
On obtient :
d)
On calcule l'intégrale :
.
ou encore on tape :
On obtient :
d)
On calcule l'intégrale :
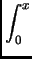 f (t)dt
f (t)dt
On tape :
On obtient :
Puis on calcule :
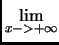
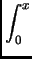 f (t)dt
f (t)dt
On tape :
On obtient :
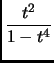 .
.
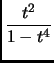 dt et
dt et
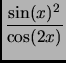 dx
dx
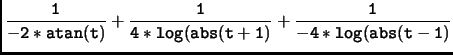
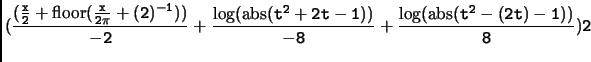
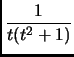 dt, et
dt, et
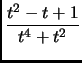 dt
dt