Les séries de Fourier

Pour obtenir le coefficient a_n (ou b_n ou c_n) de la série de Fourier d'une fonction périodique de période T, définie sur ]a, a + T[ par f (x), on mettra comme paramètre de $\tt fourier\_an$ (ou $\tt fourier\_bn$, ou $\tt fourier\_cn$) :
$\tt fourier\_an(f(x),x,T,n,a)$.
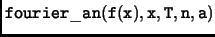Soit la fonction périodique de période 2 définie sur ] - 1, 1[ par x².
Pour calculer ses coefficients de Fourier, on tape :

$$\tt assume(n,integer)$$

$$\tt fourier\_an(x^2,x,2,n,-1)$$

On obtient :

$$\tt 4*(-1)^n/(pi^2*n^2)$$

On tape :

$$\tt fourier\_an(x^2,x,2,0,-1)$$

On obtient :

$$\tt 1/3$$

On tape :

$$\tt fourier\_bn(x^2,x,2,n,-1)$$

On obtient :

$$\tt0$$

On tape :

$$\tt fourier\_cn(x^2,x,2,n,-1)$$

On obtient :

$$\tt 2*(-1)^n/(pi^2*n^2)$$