Démarrer en calcul formel

Xcas est un logiciel libre de calcul formel. Il est téléchargeable à partir de : xcas.univ-grenoble-alpes.fr ou utilisable directement en ligne depuis xcas.univ-grenoble-alpes.fr/nw/xcasfr.html

C’est un équivalent de Maple, avec lesquel il est largement compatible. Il est possible de paramétrer Xcas pour qu’il accepte les syntaxes de Python, Maple, ou des calculatrices TI (89, Voyage 200, Nspire CAS). Nous nous limiterons à la syntaxe propre à Xcas.

Ce cours d’introduction est destiné à faciliter la prise en main de Xcas par un utilisateur connaissant un peu de mathématiques (niveau terminale S, première année d’université scientifique), et ayant une pratique minimale de l’outil informatique.

Il est hors de question d’illustrer ici toutes les possibilités de Xcas. En particulier, nous ne parlerons ni de géométrie interactive, ni de la tortue logo, ni du tableur. Pour une pratique plus avancée, on se reportera à l’aide en ligne et aux différents documents disponibles à partir de la page d’accueil du logiciel.

Le but de ce qui suit est d’aider le débutant en introduisant quelques unes des commandes les plus courantes. Il est conseillé de lire ce document après avoir lancé Xcas (depuis un onglet du navigateur pour la version sans installation, ou sous Windows, cliquer sur le raccourci xcasfr.bat, sous linux, cliquer sur Xcas dans le menu Education ou en tapant depuis un Terminal xcas & puis la touche enter, sur Mac en cliquant sur xcas dans le menu Applications), et d’exécuter les commandes proposées une par une pour en comprendre l’effet.

Table des matières

• 1  Pour commencer
  • 1.1  Interface
  • 1.2  Les commandes et l’aide en ligne
  • 1.3  Entrer des commandes
• 2  Les objets du calcul formel
  • 2.1  Les nombres
  • 2.2  Les caractères et les chaînes
  • 2.3  Les variables
  • 2.4  Les expressions
  • 2.5  Développer et simplifier
  • 2.6  Les fonctions
  • 2.7  Listes, séquences, ensembles
  • 2.8  Temps de calcul, place mémoire
• 3  Outils pour l’Analyse
  • 3.1  Dérivées
  • 3.2  Limites et développements limités
  • 3.3  Primitives et intégrales
  • 3.4  Résolution d’équations
  • 3.5  Equations différentielles
• 4  Outils pour l’Algèbre
  • 4.1  Arithmétique des entiers
  • 4.2  Polynômes et fractions rationnelles
  • 4.3  Trigonométrie
  • 4.4  Vecteurs et matrices
  • 4.5  Systèmes linéaires
  • 4.6  Réduction des matrices
• 5  Représentations graphiques
  • 5.1  Tracés de courbes
  • 5.2  Objets graphiques 2D
  • 5.3  Objets graphiques 3D
• 6  Programmation
  • 6.1  Syntaxe compatible avec Python
  • 6.2  Syntaxe en français ou compatible C/Javascript
    • 6.2.1  Le langage
    • 6.2.2  Quelques exemples
  • 6.3  Mise au point d’un programme
  • 6.4  Style de programmation
• 7  Des exercices corrigés avec Xcas
  • 7.1  Fonction et représentation graphique (niveau terminale S)
    • 7.1.1  Exercice 1
    • 7.1.2  Exercice 2
  • 7.2  Calcul de primitives (niveau début université)
  • 7.3  Dévelopements limités
  • 7.4  Équations différentielles
  • 7.5  Les matrices
• 8  Vrai ou Faux ? (d’un point de vue informatique)
• 9  Exercices (niveau université)

Index

1  Pour commencer

1.1  Interface

Pour l’instant, vous allez simplement saisir vos premières commandes. L’interface offre bien d’autres possibilités que vous découvrirez ensuite. Elle apparaît comme suit au lancement de Xcas.

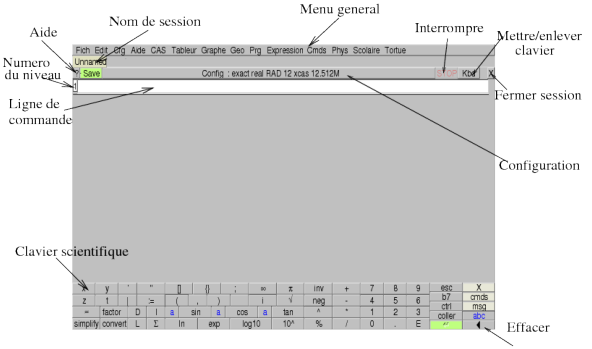
Vous pouvez la redimensionner. De haut en bas cette interface fait apparaître :

• une barre de menu cliquable : Fich, Edit, Cfg, Aide, CAS,Expression, Cmd,Prg, Graphic, Geo,Tableur,…
• un onglet indiquant le nom de la session, ou Unnamed si la session n’a pas encore été sauvegardée (on peut ouvrir plusieurs sessions en parallèle et donc avoir plusieurs onglets représentant ces sessions),
• une zone de gestion de la session avec :
  • un bouton ? pour ouvrir l’index de l’aide,
  • une barre-bouton Save pour sauvegarder la session,
  • un bouton affichant la configuration du CAS Config: exact real ... et permettant de la modifier,
  • un bouton rouge STOP permettant d’interrompre un calcul trop long,
  • un bouton Kbd pour faire apparaitre un clavier ressemblant à celui d’une calculatrice (on peut le voir ci-dessus). Il peut faciliter vos saisies, peut faire afficher une fenêtre de messages avec touche Kbd->msg (ou avec le menu Cfg->Montrer->msg) et afficher le bandeau des commandes avec la touche Kbd->cmds (ou avec le menu Cfg->Montrer->bandeau)
  • un bouton x pour fermer la session,
• une zone rectangulaire blanche numérotée 1 (première ligne de commande) dans laquelle vous pouvez taper votre première commande (cliquez si nécessaire pour faire apparaitre le curseur dans cette ligne de commande) : 1+1, suivi de la touche "Entrée" ("Enter" ou "Return" selon les claviers). Le résultat apparaît au-dessous, et une nouvelle ligne de commande s’ouvre, numérotée 2.

Vous pouvez modifier l’aspect de l’interface et sauvegarder vos modifications pour les utilisations futures (menu Cfg).

Vous n’avez pour l’instant qu’à entrer des commandes dans les lignes de commandes successives. Si vous utilisez la version html de ce cours, vous pouvez exécuter les commandes proposées en tapant sur le bouton exe. Chaque ligne de commande saisie est exécutée par la touche "Entrée". Essayez par exemple d’exécuter les commandes suivantes :
1/3+1/4; sqrt(2)^5; solve(a*x^2+b*x+c,x); 50!; exe
Toutes les commandes sont gardées en mémoire. Vous pouvez donc remonter dans l’historique de votre session pour faire afficher à nouveau des commandes antérieures avec Ctrl+$\uparrow$ pour par exemple les modifier. Essayez, par exemple, en modifiant les commandes précédentes d’exécuter aussi :

1/3+3/4;
solve(a*x+b*x+c,x);

On obtient alors

On peut alors voir apparaitre, sur la droite, une barre de scroll permettant de se déplacer dans les niveaux de la session et ici par exemple d’avoir accès au niveau 8. Le menu Edit vous permet de préparer des sessions plus élaborées qu’une simple succession de commandes. Vous pouvez créer des groupes de lignes de commandes (sections), ajouter des commentaires ou fusionner des niveaux en un seul niveau.

1.2  Les commandes et l’aide en ligne

Les commandes sont regroupées par thèmes dans les menus du bandeau supérieur : Outils, Expression,Cmds, Prg, Graphe, Geo, Tableur, Phys, Scolaire, Tortue. Certains menus sont des menus dit menus "Assistant" parce qu’ils contiennent une sélection des commandes les plus utiles, classées par thème et explicitées (menu Outils) ou parce qu’une boite de dialogue vous demande de préciser les paramètres de la commande choisie (menu Tableur$\blacktriangleright$Maths ou menu Graphic).
Les autres menus contiennent les noms des commandes : le menu Cmds contient les commandes de calcul formel, le menu Prg contient les commandes que l’on utilise en programmation, le menu Geo contient les commandes de géométrie... Lorsqu’on sélectionne une commande dans un menu,

• soit une boite de dialogue s’ouvre vous permettant de spécifier les arguments de la commande (par exemple pour tracer une courbe depuis le menu Graphe ou pour faire des statistiques depuis le menu Tableur$\blacktriangleright$Maths,
• soit la commande est recopiée dans la ligne de commande. Pour connaitre la syntaxe de cette commande, appuyez sur le bouton ? en haut à gauche, ou faites afficher la zone de Messages (en utilisant le menu Cfg->Montrer->msg).
  Vous pouvez aussi :
  • ouvrir l’index de l’aide à la commande sélectionnée (cela est automatique si on a cocher la case Aide index automatique dans le menu de configuration générale : Cfg->Configuration generale). Il faut alors cliquer sur le bouton OK pour que la commande soit recopiée dans la ligne de commande à condition que le curseur soit dans une ligne de commande.
    utoriel.tex Vous pouvez aussi cliquer sur le bouton Details pour afficher la page du manuel correspondant à la commande dans votre navigateur.
  • ouvrir automatiquement la page correspondante du manuel dans votre navigateur, en cochant la case Aide HTML automatique dans le menu de configuration générale (Cfg-> Configuration generale).

Le menu Aide contient les différentes formes d’aide possible : un guide de l’utilisateur (interface), un guide de référence (Manuels->Calcul formel, aide detaillée sur chaque commande), un Index (liste des commandes classées par ordre alphabétique avec une ligne d’entrée permettant de se déplacer facilement) et une recherche par mots clefs.

Si vous connaissez déjà le nom d’une commande et que vous désirez vérifier sa syntaxe (par exemple factor), vous pouvez saisir le début du nom de commande (disons fact) puis taper sur la touche de tabulation (située à gauche de la touche A sur un clavier français) ou cliquer sur le bouton ? en haut à gauche. L’index des commandes apparaît alors dans une fenêtre, positionné à la première complétion possible, avec une aide succinte sur chaque commande. Par exemple, vous voulez factoriser un polynôme, vous supposez que le nom de commande commence par fact, vous tapez donc fact puis la touche de tabulation, vous sélectionnez à la souris factor (ou un des exemples) puis vous cliquez sur OK.

Vous pouvez aussi saisir ?factor pour avoir l’aide succinte en réponse. Si le nom que vous avez saisi n’est pas reconnu, des commandes proches vous sont suggérées.

1.3  Entrer des commandes

L’exécution d’une ligne se fait simplement par la touche "Entrée". Si on ne souhaite pas afficher le résultat, on termine la ligne de commande par :; et on valide avec "Entrée". On peut éditer plusieurs commandes à la file avant leur exécution à condition de les séparer par un point-virgule.

Au début, de nombreuses erreurs proviennent d’une mauvaise traduction des mathématiques : Xcas ne peut pas les comprendre telles que vous les écrivez. Votre clavier vous permet de taper $ax^2+bx+c$, mais votre ordinateur ne peut pas comprendre que vous souhaitez élever $x$ au carré, le multiplier par $a$, etc…  Vous devez spécifier chaque opération, et la syntaxe correcte est a*x^2+b*x+c. La multiplication doit être notée par une étoile dans les commandes, mais est notée par un point dans les réponses. Nous insistons sur le fait que pour Xcas, ax est une variable dont le nom comporte deux lettres, et pas le produit de a par x.

Modulo quelques précautions, l’écriture des formules est assez directe. Les parenthèses ont le sens usuel pour spécifier l’ordre des opérations. Les crochets sont réservés aux listes et aux indices. Les priorités entre opérations sont standard (la multiplication est prioritaire sur l’addition, la puissance sur la multiplication). Par exemple :

• 2*a+b retourne $2\cdot a+b$
• a/2*b retourne $\displaystyle \frac{a\cdot b}{2}$
  
• a/2/b retourne $\displaystyle \frac{a}{2b}$
• a^2*b retourne $a^2\cdot b$

Dans le doute, il est toujours prudent de mettre des parenthèses pour s’assurer que l’ordre des opérations est celui souhaité.

Les commandes sont numérotées, ainsi que les réponses, mais, si vous avez modifié une ligne de commande, celle-ci garde le numéro qu’elle avait. On peut rappeler par ans() (answer) la réponse précédente c’est à dire la réponse de la dernière commande évaluée (attention, il s’agit bien de la dernière commande exécutée, qui peut ne pas être celle du niveau juste au-dessus).

2  Les objets du calcul formel

2.1  Les nombres

Les nombres peuvent être exacts ou approchés. Les nombres exacts sont les constantes prédéfinies, les entiers, les fractions d’entiers et plus généralement toute expression ne contenant que des entiers et des constantes, comme sqrt(2)*e^(i*pi/3). Les nombres approchés sont notés avec la notation scientifique standard : partie entière suivie du point de séparation et partie fractionnaire (éventuellement suivie de e et d’un exposant). Par exemple, 2 est un entier exact, 2.0 est la version approchée du même entier; 1/2 est un rationnel, 0.5 est la version approchée du même rationnel. Xcas peut gérer des nombres entiers en précision arbitraire : essayez de taper 500! et comptez le nombre de chiffres de la réponse.

On passe d’une valeur exacte à une valeur approchée par evalf, on transforme une valeur approchée en un rationnel exact par exact Les calculs sont effectués en mode exact si tous les nombres qui interviennent sont exacts. Ils sont effectués en mode approché si un des nombres est approché. Ainsi 1.5+1 renvoie un nombre approché alors que 3/2+1 renvoie un nombre exact.
sqrt(2); evalf(sqrt(2)); sqrt(2)-evalf(sqrt(2)); exact(evalf(sqrt(2)))*10^9; exact(evalf(sqrt(2)*10^9)); exe
Pour les nombres réels approchés, la précision par défaut est proche de 14 chiffres significatifs (la précision relative est de 48 bits pour les réels flottants normalisés). Elle peut être augmentée, en donnant le nombre de décimales désiré comme second argument de evalf.
evalf(sqrt(2),50); evalf(pi,100); exe
On peut aussi changer la précision par défaut pour tous les calculs en modifiant la variable Digits.
Digits:=50; evalf(pi); evalf(exp(pi*sqrt(163))); exe

La lettre i est réservée à $\sqrt{-1}$ et ne peut être réaffectée ; en particulier on ne peut pas l’utiliser comme indice de boucle.
(1+2*i)^2; (1+2*i)/(1-2*i); e^(i*pi/3); exe
Xcas distingue l’infini non signé infinity ($\infty$), de +infinity ou inf ($+\infty$) et de -infinity ou -inf($-\infty$).
1/0; (1/0)^2; -(1/0)^2 exe

2.2  Les caractères et les chaînes

Une chaîne est parenthésée par des guillemets ("). Un caractère est une chaîne ayant un seul élément.

s:="azertyuiop"; size(s); s[0]+s[3]+s[size(s)-1]; concat(s[0],concat(s[3],s[size(s)-1])); head(s); tail(s); mid(s,3,2); l:=asc(s); ss:=char(l); string(123); expr(123); expr(0123); exe

2.3  Les variables

On dit qu’une variable est formelle si elle ne contient aucune valeur : toutes les variables sont formelles tant qu’elles n’ont pas été affectées (à une valeur). L’affectation est notée :=. Au début de la session a est formelle, elle devient affectée après l’instruction a:=3, a sera alors remplacé par 3 dans tous les calculs qui suivent, et a+1 renverra 4. Xcas conserve tout le contenu de votre session. Si vous voulez que la variable a après l’avoir affectée, soit à nouveau une variable formelle, il faut la "vider" par purge(a). Dans les exemples qui suivent, les variables utilisées sont supposées avoir été purgées avant chaque suite de commandes. Il ne faut pas confondre

• le signe := qui désigne l’affectation
• le signe == qui désigne une égalité booléenne : c’est une opération binaire qui retourne 1 ou 0 (1 pour true qui veut dire Vrai et 0 pour false qui veut dire Faux)
• le signe = utilisé pour définir une équation.

a==b; a:=b; a==b; purge(a); solve(a=b,a); solve(2*a=b+1,a); exe
On peut faire certains types d’hypothèses sur une variable avec la commande assume, par exemple assume(a>2). Une hypothèse est une forme spéciale d’affectation, elle efface une éventuelle valeur précédemment affectée à la variable. Lors d’un calcul, la variable n’est pas remplacée mais l’hypothèse sera utilisée dans la mesure du possible, par exemple abs(a) renverra a si on fait l’hypothèse a>2.
sqrt(a^2); assume(0>a); sqrt(a^2); assume(n,integer); sin(n*pi); exe
La fonction subst permet de remplacer une variable dans une expression par un nombre ou une autre expression, sans affecter cette variable.
subst(a^2+1,a=1); subst(a^2+1,a=sqrt(b-1)); a^2+1; exe

Remarque avancée : pour stocker une valeur dans une variable par référence, par exemple pour modifier une valeur dans une liste (un vecteur, une matrice), sans recréer une nouvelle liste mais en modifiant en place la liste existante, on utilise l’instruction =< au lieu de :=. Cette instruction est plus rapide que l’instruction :=, car elle économise le temps de copie de la liste, mais peut avoir des effets de bord inattendus si on ne comprend pas ce qu’est un passage par référence.

2.4  Les expressions

Une expression est une combinaison de nombres et de variables reliés entre eux par des opérations : par exemple x^2+2*x+c.

Lorsqu’on valide une commande, Xcas remplace les variables par leur valeur si elles en ont une, et exécute les opérations.
(a-2)*x^2+a*x+1; a:=2; (a-2)*x^2+a*x+1; purge(a); exe
Certaines opérations de simplification sont exécutées automatiquement lors d’une évaluation :

• les opérations sur les entiers et sur les fractions, y compris la mise sous forme irréductible
• les simplifications triviales comme $x+0=x$, $x-x=0$, $x^1=x$…
• quelques formes trigonométriques comme $\cos(-x)=\cos(x)$, $\cos(\pi/4)=\sqrt{2}/2$, $\tan(\pi/4)=1$…

Nous verrons dans la section suivante comment obtenir plus de simplifications.

2.5  Développer et simplifier

En-dehors des règles de la section précédente, il n’y a pas de simplification systématique. Il y a deux raisons à cela. La première est que les simplifications non triviales sont parfois coûteuses en temps, et le choix d’en faire ou non est laissé à l’utilisateur ; la deuxième est qu’il y a en général plusieurs manières de simplifier une même expression, selon l’usage que l’on veut en faire. Les principales commandes pour transformer une expression sont les suivantes :

• expand : développe une expression en tenant compte uniquement de la distributivité de la multiplication sur l’addition et du développement des puissances entières.
• normal et ratnormal : d’un bon rapport temps d’exécution-simplification, elles écrivent une fraction rationnelle (rapport de deux polynômes) sous forme de fraction irréductible développée; normal tient compte des nombres algébriques (par exemple comme sqrt(2)) mais pas ratnormal. Les deux ne tiennent pas compte des relations entre fonctions transcendantes (par exemple comme sin et cos).
• factor : un peu plus lente que les précédentes, elle écrit une fraction sous forme irréductible factorisée.
• simplify : elle essaie de se ramener à des variables algébriquement indépendantes avant d’appliquer normal. Ceci est plus coûteux en temps et "aveugle" (on ne contrôle pas les réécritures intermédiaires). Les simplifications faisant intervenir des extensions algébriques (par exemple des racines carrées) nécessitent parfois deux appels et/ou des hypothèses (assume) pour enlever des valeurs absolues avant d’obtenir la simplification souhaitée.
• tsimplify essaie de se ramener à des variables algébriquement indépendantes mais sans appliquer normal ensuite.

Dans le menu Expression du bandeau supérieur, les sous-menus sont des menus de réécriture et contiennent d’autres fonctions, pour des transformations plus ou moins spécialisées.
b:=sqrt(1-a^2)/sqrt(1-a); ratnormal(b); normal(b); tsimplify(b); simplify(b); simplify(simplify(b)); assume(1>a); simplify(b); simplify(simplify(b)); purge(b); exe
La fonction convert permet de passer d’une expression à une autre équivalente, sous un format qui est spécifié par le deuxième argument.
convert(exp(i*x),sincos); convert(1/(x^4-1),partfrac); convert(series(sin(x),x=0,6),polynom); exe

2.6  Les fonctions

De nombreuses fonctions sont déjà définies dans Xcas, en particulier les fonctions classiques. Les plus courantes figurent dans le tableau ci-après; pour les autres, voir le menu Cmds->Reel->Special.
Sinon l’utilisateur peut définir ses propre fonctions, par exemple :

• Définition d’une fonction d’une variable :
  f(x):=x*exp(x) ou
  f:=x->x*exp(x) ou
  f:=unapply(x*exp(x),x)
• Définition de sa dérivée :
  g:=function_diff(f) ou
  g:=unapply(diff(f(x),x),x))
  ATTENTION g(x):=diff(f(x),x) N’EST PAS VALABLE ! car ce qui est à droite de := n’est pas évalué lors de la définition....il faut utiliser unapply.
• Définition d’une fonction de 2 variables :
  h(r,t):=(r*exp(t),r*t) ou
  h:=(r,t)->(r*exp(t),r*t);
• Définition à partir d’une fonction de 2 variables, d’une fonction qui à 1 variable fait correspondre une fonction:
  k(t):=unapply(h(r,t),r)
  ATTENTION Ici k(t) est une fonction de la variable r qui à r fait correspondre h(r,t). On a par exemple : k(1)(2)=(2*exp(1),2). Là aussi, il faut utiliser unapply.

Pour créer une nouvelle fonction, il faut la déclarer à l’aide d’une expression contenant la variable. Par exemple l’expression $x^2-1$ est définie par x^2-1. Pour la transformer en la fonction $f$ qui à $x$ associe $x^2-1$, trois possibilités existent :

f(x):= x^2-1;
f:=x->x^2-1;
f:=unapply(x^2-1,x);

f(x):= x^2-1; f(2); f(a^2); exe
Si f est une fonction d’une variable et E est une expression, f(E) est une autre expression. Il est essentiel de ne pas confondre fonction et expression. Si on définit : E:=x^2-1, alors la variable E contient l’expression $x^2-1$. Pour avoir la valeur de cette expression en $x=2$ il faut écrire subst(E,x=2) et non E(2) car E n’est pas une fonction. Lorsqu’on définit une fonction, le membre de droite de l’affectation n’est pas évalué. Ainsi l’écriture E:=x^2-1; f(x):=E définit la fonction $f: x \mapsto E$ car E n’est pas évalué. Par contre E:= x^2-1; f:=unapply(E,x) définit bien la fonction $f: x\mapsto x^2-1$ car E est évalué.

On peut ajouter et multiplier des fonctions, par exemple f:=sin*exp. Pour composer des fonctions, on utilise l’opérateur @ et pour composer plusieurs fois une fonction avec elle-même, on utilise l’opérateur @@.
f:=x->x^2-1; (f@f)(2); (f@sqrt)(a); f1:=f@sin; f2:=f@f; f3:=f@@3; f1(a); f2(a); f3(a); exe
On peut définir des fonctions de plusieurs variables à valeurs dans $\mathbb{R}$ comme :
f(x,y):=x+2*y
et des fonctions de plusieurs variables à valeurs dans $\mathbb{R}^p$ par exemple :
f(x,y):=(x+2*y,x-y)

2.7  Listes, séquences, ensembles

Xcas distingue plusieurs sortes de collections d’objets, séparés par des virgules :

• les listes (entre crochets)
• les séquences (entre parenthèses)
• les ensembles (entre pourcentage-accolades)

liste:=[1,2,4,2]; sequence:=(1,2,4,2); ensemble:=set[1,2,4,2]; exe
Les listes peuvent contenir des listes (c’est le cas des matrices), alors que les séquences sont plates (un élément d’une séquence ne peut pas être une séquence). Dans un ensemble, l’ordre n’a pas d’importance et chaque objet est unique. Il existe une autre structure, appelée table, dont nous reparlerons plus loin.

Il suffit de mettre une séquence entre crochets pour en faire une liste ou entre accolades précédées de % pour en faire un ensemble. On passe d’une liste à sa séquence associée par op, d’une séquence à sa liste associée en la mettant entre crochets ou avec la fonction nop. Le nombre d’éléments d’une liste est donné par size (ou nops).
se:=(1,2,4,2); li:=[se]; op(li); nop(se); nops(se); set[se]; size([se]); size(set[se]); exe
Pour fabriquer une liste ou une séquence, on utilise des commandes d’itération comme $ ou seq (qui itèrent une expression) ou makelist (qui définit une liste à l’aide d’une fonction). 1$5;k^2 $ (k=-2..2);[k^2$(k=-2..2)]
seq(k^2,k=-2..2); seq(k^2,k,-2,2); seq(k^2,k,-2,2,2); makelist(x->x^2,-2,2); [x^2 for x in range(-2,3)]; seq(k^2,k,-2,2,2); makelist(x->x^2,-2,2,2); exe
La séquence vide est notée NULL, la liste vide []. Pour ajouter un élément à une séquence il suffit d’écrire la séquence et l’élément séparés par une virgule. Pour ajouter un élément à une liste on utilise append. On accède à un élément d’une liste ou d’une séquence grâce à son indice mis entre crochets, le premier élément étant d’indice 0.

se:=NULL; se:=se,k^2$(k=-2..2); se:=se,1
li:=[1,2]; (li:=append(li,k^2))$(k=-2..2)
li[0],li[1],li[2]

Les polynômes sont souvent définis par une expression, mais ils peuvent aussi être représentés par la liste de leurs coefficients par ordre de degré décroissant, avec comme délimiteurs poly1[ et ]. Il existe aussi une représentation non symbolique pour les polynômes à plusieurs variables. Les fonctions symb2poly et poly2symb permettent de passer de la représentation expression à la représentation par liste et inversement, le deuxième argument détermine s’il s’agit de polynômes en une variable (on met le nom de la variable) ou de polynômes à plusieurs variables (on met la liste des variables).

2.8  Temps de calcul, place mémoire

Le principal problème du calcul formel est la complexité des calculs intermédiaires. Elle se traduit à la fois par le temps nécessaire à l’exécution des commandes et par la place mémoire requise. Les algorithmes implémentés dans les fonctions de Xcas sont en principe performants, mais ils ne peuvent pas être optimaux dans tous les cas. La fonction time permet de connaître le temps d’exécution d’une commande (si ce temps est très court, Xcas exécute plusieurs fois la commande pour afficher un résultat plus précis). La mémoire utilisée apparaît dans les versions Unix dans la ligne d’état (la barre-bouton). Si le temps d’exécution d’une commande dépasse quelques secondes, il est possible que vous ayez commis une erreur de saisie. N’hésitez pas à interrompre l’exécution (bouton rouge STOP en haut à droite, il est conseillé de faire une sauvegarde de votre session auparavant).

3  Outils pour l’Analyse

3.1  Dérivées

La fonction diff permet de calculer la dérivée d’une expression par rapport à une ou plusieurs de ses variables. Pour dériver une fonction $f$, on peut appliquer diff à l’expression $f(x)$, mais alors le résultat est une expression. Si on souhaite définir la fonction dérivée, il faut utiliser function_diff.
E:=x^2-1; diff(E); f:=unapply(E,x); diff(f(x)); f1:=function_diff(f);f1(x); exe
Il ne faut pas définir la fonction dérivée par f1(x):=diff(f(x)), car dans cette définition, x aurait deux sens incompatibles : c’est d’une part la variable formelle de dérivation et d’autre part l’argument de la fonction f1. D’autre part, cette définition évaluerait diff à chaque appel de la fonction (car le membre de droite d’une affectation n’est jamais évalué), ce qui serait inefficace.
Il faut utiliser f1:=function_diff(f), ou f1:=unapply(diff(f(x)),x).

La fonction diff s’applique à n’importe quelle combinaison de variables, et permet de calculer des dérivées partielles successives.
E:=sin(x*y); diff(E,x); diff(E,y); diff(E,x,y)-diff(E,y,x); simplify(ans()); diff(E,x,2) exe
Si le deuxième argument de diff est une liste, une liste de dérivées est retournée. Par exemple pour calculer le gradient de $\sin(xy)$ : diff(sin(x*y),[x,y]) (on peut aussi utiliser grad). Des commandes particulières permettent de calculer les combinaisons classiques de dérivées partielles.

3.2  Limites et développements limités

La fonction limit calcule les limites finies ou infinies, quand elles existent. On peut demander une limite à gauche ou à droite à l’aide d’un quatrième argument (+1 ou -1). Quand la fonction dépend d’un paramètre, la limite obtenue peut dépendre des hypothèses faites, avec la fonction assume, sur ce paramètre.
limit(1/x,x,0); limit(1/x,x,0,1); limit(1/x,x,0,-1); limit(a/x,x,0,1); assume(a>0); limit(a/x,x,0,1); exe
Pour les développements limités, deux fonctions sont disponibles, series et taylor. La différence est que l’ordre du développement doit être spécifié pour series, il est égal à 6 par défaut pour taylor.

L’ordre du développement limité demandé est utilisé par Xcas en interne pour faire ses développements. En cas de simplifications, l’ordre du développement obtenu pourra être inférieur, il faudra alors recommencer le calcul avec un ordre plus grand. L’expression retournée est constituée du polynôme de Taylor, plus un reste dans lequel apparaît une fonction order_size qui est presque toujours un $O$ (i.e. une fonction bornée, plus précisément si la fonction order_size tend vers l’infini, elle le fait lentement, en vérifiant pour tout $a>0$, $x^a$order_size($x$) tend vers $0$ quand $x$ tend vers $0$). Pour supprimer le reste et ne garder que le polynôme de Taylor, on peut utiliser convert avec l’option polynom.
taylor(1/(x^2+1),0); taylor(1/(x^2+a^2),x=0); series(1/(x^2+1),0,11); series(1/(x^2+1),+infinity,11); series(tan(x),pi/4,3); series(sin(x)^3/((1-cos(x))*tan(x)),0,4); series(sin(x)^3/((1-cos(x))*tan(x)),0,6); series(tan(sin(x))-sin(tan(x)),0,13); convert(ans(),polynom); series(f(x),0,3); g:=f@f; series(g(x),0,2); exe

3.3  Primitives et intégrales

La fonction integrate calcule une primitive d’une expressionpar rapport à $x$ ou par rapport à la variable donnée en argument. Si l’expression comporte plusieurs variables, il vaut préciser la variable d’intégration. Si on ajoute deux arguments $a$ et $b$ après la variable d’intégration, on calcule l’intégrale sur l’intervalle $[a,b]$. Eventuellement les bornes de l’intégrale peuvent être des expressions, ce qui permet de calculer des intégrales multiples.
integrate(x^2-1); integrate(x^2-1,x,-1,1); integrate(x*y,x); integrate(x*y,y,0,x); integrate(integrate(x*y,y,0,x),x,0,1); exe
Pour calculer une intégrale, un logiciel de calcul formel recherche une primitive puis l’évalue entre les bornes, afin d’obtenir une valeur exacte. Dans certains cas, il est inutile de calculer une primitive, soit parce qu’il n’en existe pas qui s’exprime avec les fonctions élémentaires, soit parce qu’un calcul numérique est plus adapté (par exemple si le temps de calcul de la primitive est trop long, si la fonction présente des singularités dans l’intervalle d’intégration, etc…). Dans ce cas, on demande une valeur approchée en utilisant evalf, ou bien on utilise directement la fonction romberg, qui est appelée par evalf.
integrate(exp(-x^2)); integrate(exp(-x^2),x,0,10); evalf(integrate(exp(-x^2),x,0,10)); gaussquad(exp(-x^2),x,0,10); evalf(sqrt(pi)); exe

3.4  Résolution d’équations

Comme pour les intégrales on distingue :

• la résolution exacte qui renvoie toutes les solutions lorsque c’est possible (par exemple pour certaines équations polynomiales ou s’y ramenant)
• la résolution approchée qui calcule par un algorithme itératif une valeur proche d’une des solutions.

La résolution exacte s’effectue à l’aide de solve, dont le premier argument est une équation. Le membre de droite est supposé nul s’il n’est pas précisé. Par défaut solve ne retourne pas les solutions complexes. Pour les obtenir, il faut cocher Complexe dans la configuration du CAS (Cfg->Configuration de CAS ou sur la barre-bouton Config :exact...)
Exécutez les commandes suivantes avant et après avoir activé l’option Complex.
solve(x^2-a*x+2,x); solve(x^2+2,x); solve(x^3=1,x); exe
Les racines exactes sont calculées pour les polynômes de degré 1 et 2 (les formules de Cardan et Ferrari pour les degrés 3 et 4 ne sont pas utilisées, car les solutions obtenues ne sont pas facilement maniables). En degré supérieur, la fonction solve affiche un message d’erreur et renvoie une liste vide.

Pour les équations trigonométriques, les solutions principales sont renvoyées. Pour obtenir toutes les solutions, il faut activer l’option All_trig_sol. Comparer les commandes suivantes avec et sans cette option. solve(cos(x),x); solve(cos(x)+sin(x),x); exe

La fonction solve peut aussi résoudre des systèmes d’équations. Le premier argument est la liste des équations, le second est la liste des variables.
solve([x^2+y-2,x+y^2-2],[x,y]) exe

La fonction de résolution approchée est fsolve. Elle propose en option différents algorithmes (menus Calc->Num_solve_eq et Calc->Num_solve_syst). Le plus célèbre est l’algorithme de Newton, qui a de multiples variantes. Le principe général de tous ces algorithmes est de calculer les termes successifs d’une suite qui converge vers une solution de l’équation ou du système proposé. Il faut pour cela choisir selon les cas un point de départ, ou un intervalle de recherche.
fsolve((x^5+2*x+1)=0,x,1,newton_solver); newton(x^5+2*x+1,x,1.0); newton(x^5+2*x+1,x,1+i); newton(x^5+2*x+1,x,-1+i); exe

3.5  Equations différentielles

Comme dans les deux sections précédentes, on distingue le calcul exact, qui n’est pas toujours possible, du calcul approché. La résolution exacte s’effectue par desolve. Les dérivées de la fonction inconnue $y$ peuvent s’écrire $y'$, $y''$, qui sont traduits en diff(y), diff(diff(y)). Si on ne spécifie pas de condition initiale, le résultat est donné en fonction de constantes arbitraires.
desolve(y'=y,y); desolve(y''+2*y'+y=0,y); desolve((x^2-1)*y'+2*y=0,y); exe
Les conditions initiales sont vues comme des équations supplémentaires, qui forment une liste avec l’équation différentielle.
desolve([y'=y,y(0)=1],y); desolve([y''+2*y'+y=0,y(0)=1],y); desolve([y''+2*y'+y=0,y(0)=1,y'(0)=1],y); desolve([y''+2*y'+y=0,y(0)=1,y(1)=0],y); desolve([(x^2-1)*y'+2*y=0,y(0)=1],y); desolve((t^2-1)*diff(y(t),t)+2*y(t)=0,y(t)); exe

La fonction odesolve permet de résoudre par des méthodes numériques une équation différentielle $y'=f(x,y)$ passant par un point $(x_0,y_0)$. Par exemple
odesolve(sin(x*y),[x,y],[0,1],2) exe
permet de calculer $y(2)$ où $y(x)$ est la solution de $y'(x)=\sin(xy)$, telle que $y(0)=1$. La fonction plotode représente graphiquement la solution d’une équation différentielle, plotfield représente le champ des tangentes. La fonction interactive_odeplot représente le champ des tangentes et permet de cliquer sur le graphique pour tracer les solutions passant par les points cliqués. plotfield(sin(x*y),[x,y]); plotode(sin(x*y),[x,y],[0,1]); exe

erase()
interactive_plotode(sin(x*y),[x,y])

4  Outils pour l’Algèbre

4.1  Arithmétique des entiers

Les opérations sur les entiers figurent dans le menu Cmds->Entier. Les calculs modulo $p$ se font en utilisant % p. Une fois défini un entier modulo $p$, disons a:=3%5, tous les calculs seront efffectués dans $\Z/p\Z$ : a*2 renvoie 1%5 (6 modulo 5), 1/a renvoie 2%5, …  Pour calculer efficacement les puissances modulo $p$, on peut utiliser ce qui précède, ou la fonction powermod ou powmod. a:=3 mod 5; a+12; a^4; powermod(3,4,5); exe

4.2  Polynômes et fractions rationnelles

Les fonctions de traitement des polynômes sont dans le menu Cmds->Polyn\^omes.

On utilise normal ou expand pour développer, ou plus généralement mettre une fraction sous forme irréductible, et factor pour factoriser. Le résultat dépend du corps de nombres dans lequel on se place. Par défaut il s’agit des rationnels si les coefficients sont exacts ou des réels sinon. Pour les complexes (exacts ou approchées), il faut activer l’option Complexe à partir du bouton rappelant la configuration Config:.... On peut aussi déclarer les coefficients comme des entiers modulo $p$ pour travailler dans $\Z/p\Z$ (commande %) ou dans un corps fini (défini par la commande GF). Exécutez les commandes suivantes avant et après avoir activé l’option Complexe.
P:=x^4-1; factor(P); gcd(P,x^3-1); divis(P); propfrac(x^4/P); partfrac(4/P); Q:=(x^4+1) mod 3; factor(Q); purge(g); GF(2,8); // corps fini a 2^8 elements factor(g^3*x^2+1); genpoly(5,3,x); genpoly(2,3,x); genpoly(2*y+5,3,x); exe

4.3  Trigonométrie

Le menu Cmds->R\'eel->Transcendental contient les fonctions circulaires et hyperboliques ainsi que leurs inverses. Pour linéariser et développer on utilise tlin et texpand. Beaucoup d’autres réécritures sont accessibles à partir des menus

• Expression->Trigo : transformations en $\tan(x/2)$ (halftan), transformation des tangentes en sinus et cosinus (tan2sincos), …
• Expression->Trigo exp : transformation des fonctions trigonométriques en exponentielles par les formules d’Euler (trig2exp), transformation des exponentielles en fonctions trigonométriques (exp2trig), transformation des exponentielles en puissances (exp2pow)...,
• Expression->Trigo inv : transformation des fonctions inverses

exp2pow(exp(3*ln(x))); exp2trig(exp(i*x)); trig2exp(cos(x)); E:=sin(x)^4+sin(x)^3; El:=tlin(E); texpand(El); tsimplify(E); tsimplify(El); tsimplify(E-El); halftan(E); trig2exp(El); Et:=trigtan(E); tan2sincos(Et); tan2sincos2(Et); tan2cossin2(Et); exe

4.4  Vecteurs et matrices

Un vecteur est une liste de nombres, une matrice est la liste de ses vecteurs lignes. Le produit matriciel est noté comme le produit ordinaire *. Les vecteurs sont a priori des vecteurs lignes, mais le produit à droite par un vecteur ligne est effectué comme si c’était une colonne. En particulier, si v et w sont deux vecteurs de même taille, v*w retourne leur produit scalaire.
A:=[[1,2,3],[4,5,6],[7,8,9]]; v:=[1,1,1]; v*v; A*v; v*A; B:=[[1,1,1],[2,2,2]]; // A*B; // erreur B*A; A*tran(B); exe
À partir d’une fonction qui à deux indices $(j,k)$ associe un réel $a(j,k)$, on peut constituer une matrice avec makemat ou matrix. Pour makemat les indices commencent à 0, pour matrix il commencent à 1.
makemat((j,k)->j+2*k,3,2); matrix(3,2,(j,k)->j+2*k); exe
On peut aussi créer des matrices par blocs avec la commande blockmatrix.
A:=makemat((j,k)->j+2*k,3,2); B:=idn(3); blockmatrix(1,2,[A,B]); blockmatrix(2,2,[A,B,B,A]); exe
On accède à un élément d’une matrice grâce à deux indices séparés par une virgule et mis entre crochets. Le premier indice est l’indice de la ligne et le deuxième celui de la colonne. Les indices commencent à 0. Par exemple, si A:=[[0,2],[1,3],[2,4]] alors A[2,1] renvoie 4. Pour extraire un bloc de la matrice, on utilise des intervalles comme indices : A[1..2,0..1] renvoie le bloc constitué des lignes 1 à 2 et des colonnes 0 à 1.

Notez que les matrices de Xcas sont recopiées entièrement à chaque modification d’un coefficient. Ceci est pénalisant si on modifie successivement dans un programme beaucoup de coefficients d’une même (grande) matrice.

4.5  Systèmes linéaires

La fonction linsolve résout une liste d’équations linéaires, avec la même syntaxe que solve. On peut aussi utiliser simult pour résoudre plusieurs systèmes d’équations linéaires qui ne diffèrent que par leur second membre, en mettant comme premier argument la matrice du système et comme second argument la matrice dont la (ou les) colonnes sont le (ou les) second membre(s) des systèmes, ou bien rref d’argument une matrice obtenue en bordant la matrice du système avec lesecond membre (border(A,tran(b)) si b est une matrice colonne). Quand le système est impossible, linsolve retourne la liste vide, simult retourne un message d’erreur, rref retourne une matrice dont une des lignes est nulle, sauf le dernier coefficient. Quand le système est indéterminé, linsolve retourne la solution fonction de certaines variables, simult retourne seulement une solution, rref retourne une matrice dont une ou plusieurs lignes sont nulles. L’exemple ci-dessous concerne le système $$\left\{ \begin{array}{llllllr} x &+& y &+& az&=&1\\ x & +& a y&+& z&=&1 \\ ax & +&y &+& z&=&-2 \end{array}\right.$$ Il a une solution unique pour $a\neq 1$ et $a\neq -2$, il est impossible pour $a=1$ et il est indéterminé pour $a=-2$.
a:='a'; linsolve([x+y+a*z=1,x+a*y+z=1,a*x+y+z=-2],[x,y,z]); a:=1; linsolve([x+y+a*z=1,x+a*y+z=1,a*x+y+z=-2],[x,y,z]); a:=-2; linsolve([x+y+a*z=1,x+a*y+z=1,a*x+y+z=-2],[x,y,z]); purge(a); exe

A:=[[1,1,a],[1,a,1],[a,1,1]]; solve(det(A),a); A1:=subst(A,a=1); rank(A1); image(A1); ker(A1); A2:=subst(A,a=-2); rank(A2); image(A2); ker(A2); exe

b:= [1,1,-2]; B:=tran(b); simult(A,B); //simult(A1,B); // erreur //simult(A2,B); // erreur M:=blockmatrix(1,2,[A,B]); rref(M); rref(border(A,b)); rref(border(A1,b)); rref(border(A2,b)); exe

4.6  Réduction des matrices

La fonction jordan prend en entrée une matrice $A$ et retourne en sortie une matrice de passage $P$ et une forme réduite de Jordan $J$ telles que $P^{-1}A P=J$. Soit $A$ est diagonalisable auquel cas $J$ est diagonale et contient les valeurs propres de $A$ sur la diagonale, soit $A$ n’est pas diagonalisable et $J$ comporte des "1" ou des "0" au-dessus de la diagonale. Pour les matrices exactes et symboliques, seules les valeurs propres calculables par solve sont accessibles. Pour des matrices de nombres approchés, un algorithme numérique est utilisé, et il risque d’échouer en cas de valeurs propres multiples ou très proches. La matrice $A$ de l’exemple qui suit a pour valeurs propres doubles 1 et 2. Elle est diagonalisable pour $a=0$, non diagonalisable pour $a\neq 0$.
purge(a); A:=[[1,1,-1,0],[0,1,0,a],[0,-1,2,0],[1,0,1,2]]; factor(poly2symb(simplify(pcar(A)))); jordan(A); eigenvals(A); // eigenvects(A); exe

jordan(subs(A,a=0)); jordan(subs(A,a=1)); jordan(evalf(subs(A,a=0))); jordan(evalf(subs(A,a=1))); exe
Certaines fonctions, définies par des séries entières, s’étendent aux matrices dès lors que l’on sait calculer leur forme de Jordan. La plus utile est l’exponentielle.
A:=[[0,1,0],[0,0,1],[-2,1,2]]; jordan(A); exp(A); ln(A); sin(A); exe

5  Représentations graphiques

Pour obtenir une représentation graphique dans Xcas, il faut saisir une commande dont la sortie est un objet graphique. Pour vous aider à effectuer les représentations graphiques les plus courantes, le menu Graphic vous propose des boites de dialogue qui se chargent de créer une ligne de commande et de le valider pour afficher le graphique souhaité.

Si vous souhaitez représenter plusieurs objets graphiques dans une même représentation, vous devez séparer les commandes les créant par un ;. Vous pouvez aussi créer une figure (menu Geo, Nouvelle figure) et utiliser le menu Geo pour créer des objets géométriques.

Chaque commande graphique crée un objet graphique 2-d ou 3-d, qui est traduit en réponse par une image dans la fenêtre Xcas. A droite de cette image, des boutons de zoom in et out permettent d’agrandir ou de rapetisser la représentation, des flèches permettent de la déplacer.

Les paramètres par défaut (en particulier les intervalles de représentation en abscisse et ordonnée) peuvent être changés dans la fenêtre de configuration graphique accessible depuis le menu Cfg->Configuration graphique.

Notez enfin que les objets graphiques 2-d sont aussi affichés dans une fenêtre appelée DispG (Display Graphics) que vous pouvez faire apparaître par le menu Cfg->Montrer->DispG ou avec la commande DispG. La différence est que les graphiques successifs sont tracés individuellement dans chaque fenêtre de réponse, alors qu’ils sont superposés dans la fenêtre DispG. Vous pouvez effacer la fenêtre DispG par la commande ClrGraph.

5.1  Tracés de courbes

Pour créer rapidement des tracés de courbes simples, il est conseillé d’utiliser le menu Graphe.

L’instruction de tracé d’une courbe représentative de fonction est plot avec en paramètres une expression ou une liste d’expressions dont on veut la représentation graphique, puis la variable (éventuellement on indique l’intervalle de valeurs de la variable). Pour distinguer plusieurs courbes, on peut utiliser un troisième argument par exemple couleur= suivi de la liste des couleurs à utiliser. Les couleurs peuvent être codées par leur nom français, leur nom anglais ou leur numéro. La fonction couleur change la couleur de base pour toutes les fonctions graphiques qui suivent. La fonction tangent permet d’obtenir la tangente à une courbe en un point. E:=(2*x+1)/(x^2+1);plot(E) exe
plot(E,x=-2..2,color=red) exe
couleur(vert); plot(E,couleur=rouge); tangent(plot(E),0) exe
plot([sin(x),x,x-x^3/6], x=-2..2,couleur=[rouge,bleu,vert]) exe
li:=[(x+k*0.5)^2 for k in range(-5,6)]:; plot(li,x=-8..8,couleur=range(11)) exe

La fonction plotparam permet d’effectuer le tracé de $(x(t),y(t))$. Il faut définir les deux coordonnées comme une seule expression complexe dont $x(t)$ est la partie réelle et $y(t)$ la partie imaginaire. La fonction plotpolar trace les courbes en coordonnées polaires. La commande plotimplicit(f(x,y),x,y) trace l’ensemble des solutions de $f(x,y)=0$. plotparam(sin(t)^3+i*cos(t)^3,t,0,2*pi) exe
plotparam(t^2+i*t^3,t,-1,1) exe
plotpolar(1/(1-2sin(t/2)),t,0,4*pi) exe
gl_x=-7..7; gl_y=-7..7; plotpolar(tan(t)+tan(t/2),t,0,2*pi,tstep=0.02) exe
plotimplicit(x^2+4*y^2-4,x,y) exe

5.2  Objets graphiques 2D

Xcas étant aussi un logiciel de géométrie plane, de nombreuses figures peuvent être tracées (dans un écran que l’on obtient avec Alt+g) par des commandes du menu Geo, par exemple des polygones, des coniques…  Les arguments de ces commandes sont souvent des points (commande point) qui peuvent en général être saisis directement par leur affixe complexe. Par exemple cercle(2+3*i,2) trace le cercle centré au point $(2,3)$, de rayon 2. La commande legende permet de placer un texte à un endroit, lui aussi spécifié par un nombre complexe. Les fonctions polygonplot et scatterplot prennent en entrée une liste d’abscisses et une liste d’ordonnées. lx:=range(1,11); ly:=apply(sin,lx); polygonplot(lx,ly); exe
scatterplot(lx,ly) exe
polygone_ouvert(lx+i*ly) exe

5.3  Objets graphiques 3D

• Pour tracer une surface définie par l’équation $z=f(x,y)$, on utilise la commande plotfunc, avec en arguments l’équation de la surface et la liste des deux variables. On peut aussi indiquer la plage de variable, et la discrétisation. plotfunc(x^2-y^2,[x,y]) exe
  plotfunc(x+y^2,[x=-5..5,y=-2..2], xstep=0.5,ystep=0.1,affichage=vert+rempli) exe
  On obtient une surface en dimension 3. Pour modifier le point de vue, utilisez la souris en-dehors du cube de visualisation ou cliquez dans la figure 3-d, puis utilisez les touches x,X,y,Y,z,Z (rotations par rapport aux axes), + et - pour les zooms, les flèches de direction et page up/down pour changer la fenêtre de visualisation (la fenêtre de calcul par défaut est définie par la configuration graphique si on ne l’a pas indiquée en paramètre dans plotfunc)
• On peut aussi tracer une surface paramétrée avec plotparam dont le premier argument est une liste de taille 3 contenant les coordonnées du point et les 2 arguments suivants les paramètres : plotparam([u,v,u+v],u=-1..1,v=-2..2) exe
  
• Pour tracer des courbes paramétrées dans l’espace, on utilise aussi la commande plotparam mais avec un seul paramètre : plotparam([u,u^2,u^3],u=-1..1) exe
  
• On peut aussi tracer des objets géométriques 3D dans une figure 3-d que l’on obtient avec Alt+h, puis en utilisant des commandes du menu Geo, par exemple : point, droite ,plan, polygone, sphere… plan(z=x+y); droite(x=y,z=y); A:=point(1,2,3); B:=point(2,-1,1); C:=point(1,0,0); plan(A,B,C,couleur=cyan); droite(A,B,affichage=line_width_3) exe
  

6  Programmation

6.1  Syntaxe compatible avec Python

Comme Python est imposé dans l’enseignement secondaire, Xcas permet maintenant l’écriture de programmes avec une syntaxe largement compatible avec Python, ce qui évite d’avoir à apprendre un autre langage.

Vérifiez dans la configuration du CAS (menu Cfg ou directement affichage dans la barre d’état) que vous êtes en mode Xcas Python. Il est conseillé de conserver ^ comme équivalent du signe puissance (^==**). Voici par exemple un programme calculant le PGCD de 2 entiers écrit en syntaxe Python :

def pgcdi(a,b):
  while b!=0:
    r=irem(a,b)
    a=b
    b=r
  return a

exe
pgcdi(15,25) exe
On a utilisé ici l’instruction irem(a,b) pour calculer le reste de la division de $a$ par $b$ plutôt que a % b car dans certains modes de Xcas, a % b renvoie la classe de $a$ dans $\mathbb{Z}/b\mathbb{Z}$.

6.2  Syntaxe en français ou compatible C/Javascript

Cette section s’adresse aux personnes qui ne connaissent pas Python ou ne souhaitent pas utiliser la syntaxe compatible Python.

6.2.1  Le langage

Xcas permet d’écrire des programmes, comme n’importe quel langage de programmation. Voici ses principales caractéristiques.

• C’est un langage fonctionnel. L’argument d’une fonction peut être une autre fonction. Si c’est le cas, on peut soit donner le nom de la fonction argument dans la commande, soit sa définition : par exemple function_diff(f) ou bien function_diff(x->x^2).
• Il n’y a pas de distinction entre programme et fonction : une fonction renvoie la valeur de la dernière instruction évaluée ou ce qui suit le mot réservé return. Comme pour tous les environnements de calcul, programmer consiste à étendre Xcas en lui rajoutant les fonctions souhaitées. Structurer la programmation consiste à hiérarchiser les différentes fonctions qui s’appellent entre elles.
• Le langage est non typé. On distingue seulement les variables globales, qui ne sont pas déclarées, et les variables locales, déclarées en début de fonction.

Dans un programme, lorsqu’on appelle une variable munie d’un indice qui n’est pas affectée à une liste, séquence ou matrice, c’est une table qui est créée, et non une liste. Une table est un conteneur d’objets analogue aux listes et aux séquences. La différence est qu’elle peut être indicée par autre chose qu’un entier, par exemple une chaîne de caractères…  Si a est une variable formelle, la commande a[4]:=2 crée une table a.
Pour que a soit une liste, il faut d’abord affecter a à une liste par exemple a:=[0$10] (si la taille de la liste est connue) ou a:=[] puis a[4]:=2. Même si le langage est non typé, il est donc recommandé d’initialiser les variables avant de les utiliser. La syntaxe de déclaration d’une fonction est la suivante.

nom_fonction(var1,var2,...):={
local var_loc1, var_loc2,... ;
  instruction1;
  instruction2;
  ...
}

La syntaxe est soit avec des mots clef en français soit comme en langage C/Javascript, soit en syntaxe compatible Python

Pour les tests, une condition est un booléen, résultat d’une expression logique, utilisant les opérateurs habituels.

Attention, i désigne $\sqrt{-1}$ et ne peut pas être utilisé comme variable de boucle. L’instruction break; permet de sortir d’une boucle et continue; de passer immédiatement à l’itération suivante. De nombreuses variantes sont reconnues en particulier en mode de compatibilité avec Maple, Mupad et les TI89/Voyage 200. On peut capturer des erreurs d’exécution par

try {bloc_erreurs_capturees} 
catch (variable)
    {bloc_execute_si_erreur}

Par exemple :

try{A:=idn(2)*idn(3)} 
catch(erreur) 
{print("l'erreur est "+erreur)}

6.2.2  Quelques exemples

Pour écrire un programme, il est conseillé d’ouvrir un éditeur de programme avec le menu Prg->Nouveau programme. Le menu Prg de l’éditeur permet d’entrer facilement les structures de programmation. On peut ensuite sauvegarder le texte du programme indépendamment de la session de travail pour l’utiliser ensuite dans une autre session de travail.

Voici deux versions du calcul du PGCD de deux entiers, une version itérative, puis une version récursive.

Vous pouvez saisir une fonction, par exemple pgcdi, dans un niveau éditeur de programme de Xcas (Prg->Nouveau programme). Vous pouvez tester la syntaxe (bouton OK). Vous pouvez ensuite utiliser cette fonction dans une ligne de commande, en tapant par exemple pgcdi(25,15). Pour utiliser cette fonction dans une autre session Xcas, vous pouvez la sauvegarder par exemple sous le nom pgcdi.cxx, en utilisant la commande read("idiv2.cxx") ou en l’ouvrant depuis un éditeur de programme (et en le validant par OK).

6.3  Mise au point d’un programme

Il arrive parfois qu’un programme ne fonctionne pas du premier coup comme prévu (!) Il est alors possible de l’exécuter en mode pas-à-pas pour le mettre au point, avec la commande debug. Pour plus de détails consulter le menu Aide->Interface. Par exemple, pour le programme idiv2, on lance la mise au point en tapant :
debug(pgcdi(25,15))
Le débuggueur affiche automatiquement la valeur des paramètres a,b puis des variables locales (ici r) lors de l’exécution instruction par instruction avec le bouton sst.

6.4  Style de programmation

Xcas est interprété et non compilé. Plus que le nombre de lignes du programme, c’est le nombre d’instructions réellement exécutées qui influence le temps de calcul. En règle générale, il est plus rapide de créer des listes ou des séquences que de programmer des boucles. Voici quelques manières de calculer $5000!$ : comparez leurs temps d’exécution. 5000!:; exe
product(range(1,5001)):; exe
product(cumSum(seq(1,5000))):; exe
f:=1; (f:=f*n)$(n=2..5000):; exe
f:=1; for(n:=1;n <= 5000;n++) {f:=f*n}
f:=1;n:=1; while(n < 5000) {n:=n+1; f:=f*n}
f:=1; (f:=f*n)$(n=2..5000):; La rapidité d’exécution est parfois contradictoire avec la clarté du programme, et on doit accepter des compromis. Dans une utilisation courante, le temps de calcul n’est pas réellement un enjeu : on utilise en général les langages interprétés comme Xcas pour tester des algorithmes et réaliser des maquettes. Les applications en vraie grandeur sont codées dans des langages compilés comme C++ (en utilisant par exemple la librarie giac pour les fonctions de calcul formel).

7  Des exercices corrigés avec Xcas

7.1  Fonction et représentation graphique (niveau terminale S)

7.1.1  Exercice 1

On considère la fonction $f$ de $\mathbb{R}$-{3} dans $\mathbb{R}$ définie par : $$f(x)=(x+1)\ln|x-3|$$

1. Calculer la derivée première $f'$ et seconde $f''$ de $f$.
   En déduire les variations de $f'$.
2. Calculer les limites de $f'$ en $-\infty$ et en 3 à gauche.
3. Montrer que $f'$ s’annule une seule fois en $\alpha$ sur $]-\infty;3[$. Donner un encadrement de $\alpha$ d’amplitude 0.1.
4. Étudier le signe de $f'(x)$ sur $\mathbb{R}$-{3} et en déduire les variations de $f$.
5. Tracer la courbe $C$ de $f$ dans un repère orthonormé (unité 1$cm$).
6. Calculer l’aire en $cm^2$ de la région comprise entre $C$, l’axe des abscisses et les droites d’équations $x=-1$ et $x=2$.

Réponses

1. On tape pour définir la fonction $f$ :
   f(x):=(x+1)*ln(abs(x-3))
   On tape pour définir la fonction $f'$ :
   f1:=function_diff(f):;
   puis,
   f1(x)
   On obtient :
   ln(abs(x-3))+(x+1)/(x-3)
   Donc $\displaystyle f'(x)=\ln(|x-3|)+\frac{x+1}{x-3}$.
   On tape pour définir la fonction $f''$ :
   f2:=function_diff(f1):;
   puis,
   f2(x)
   On obtient :
   1/(x-3)+1/(x-3)+(x+1)*(-(1/((x-3)^2)))
   puis pour simplifier l’écriture, on tape :
   normal(f2(x))
   On obtient :
   (x-7)/(x^2-6*x+9)
   ou bien pour factoriser, on tape :
   factor(f2(x))
   On obtient :
   (x-7)/((x-3)^2)
   Donc $\displaystyle f''(x)= \frac{x-7}{(x-3)^2}$

   Autre façon
   On tape pour définir la fonction $f$ :

   f(x):=(x+1)*ln(abs(x-3))

   On tape pour calculer $f'(x)$ :

   dfx:=diff(f(x)

   On obtient :

   ln(abs(x-3))+(x+1)/(x-3)

   Donc $\displaystyle f'(x)=\ln(|x-3|)+\frac{x+1}{x-3}$.
   Et on tape pour définir la fonction $f'$ à partir de dfx:

   f1:=unapply(dfx,x);

   On tape pour calculer $f''(x)$ :

   ddfx:=diff(dfx)

   On obtient :

   1/(x-3)+1/(x-3)+(x+1)*(-(1/((x-3)^2)))

   ou pour avoir une écriture factorisée, on tape directement :

   ddfx:=factor(diff(dfx))

   On obtient :

   (x-7)/((x-3)^2)

   Donc $\displaystyle f''(x)= \frac{x-7}{(x-3)^2}$
   Et on tape pour définir la fonction $f''$ à partir de ddfx:

   f2:=unapply(ddfx,x);

   Cette façon de faire à l’avantage de définir la fonction $f2=f''$ à partir d’une expression simplifiée ou factorisée.
   Attention !!! On ne peut pas écrire par exemple :
   g(x):=normal(diff(f(x))) pour définir la fonction $g=f'$ mais on doit écrire g:=unapply(normal(diff(f(x))),x) car sinon il y a confusion entre $x$ variable de dérivation et $x$ variable de la fonction $g$.

2. On tape pour avoir la limite de $f'$ en $-\infty$ :
   limit(f1(x),x,-infinity)
   On obtient :
   +infinity
   On tape pour avoir la limite de $f'$ en $3^-$ :
   limit(f1(x),x,3,-1)
   On obtient :
   -infinity
3. $f'$ est continue et décroissante de $+\infty$ à $-\infty$ sur $]-\infty;3[$ puisque $f''(x)<0$ sur $]-\infty;3[$. Il existe donc $\alpha$ unique dans $]-\infty;3[$ tel que $f'(\alpha)=0$.
   On tape pour avoir une valeur approchée de $\alpha$ :
   assume(x<3);fsolve(f1(x),x)
   On obtient :
   x,0.776592890991
   Puis, on tape pour enlever l’hypothèse sur $x$ :
   purge(x)
   On tape :
   f1(0.7)
   On obtient :
   0.0937786881525
   On tape :
   f1(0.8)
   On obtient :
   -0.0297244578175
   On a $f1(0.7)>0$ et $f1(0.8)<0$ donc $0.7<\alpha<0;8$.
4. Puisque $f''(7)=0$, on tape pour avoir le minimum de $f'$ sur $]3;+\infty[$ :
   f1(7)
   On obtient :
   ln(4)+2
   Le minimum de $f'$ sur $]3;+\infty[$ est donc positif.
   Donc $f'(x)>0$ si $x \in\ ]-\infty;\alpha[\ \cup \ ]3;+\infty[\$ et $f'(x)<0$ si $x \in\ ]\alpha;3[$.
   Donc $f$ est croissante sur $\ ]-\infty;\alpha[\ \cup \ ]3;+\infty[\$ et est décroissante sur $\ ]\alpha;3[$.
5. On cherche les limites de $f$ en $-\infty$, $+\infty$, et en $3$.
   On tape :
   limit(f(x),x,-infinity)
   On obtient :
   -infinity
   On tape :
   limit(f(x),x,+infinity)
   On obtient :
   +infinity
   On tape :
   limit(f(x),x,3)
   On obtient :
   -infinity
   On trace les graphes de $f$ et des deux droites $x=-1$ et $x=2$, on tape :
   plofunc(f(x),x);droite(x=1);droite(x=2)
   On obtient le tracé du graphe de $f$ et le tracé des droites $x=-1$ et $x=2$.
6. On tape pour trouver l’aire en $cm^2$ :
   integrate(f(x),x,-1,2)
   On obtient :
   8*ln(4)-12+15/4
   On tape :
   normal(8*ln(4)-12+15/4))
   On obtient :
   8*ln(4)-33/4
   On tape si on veut faire l’intégration par parties :
   ibpu((x+1)*ln(abs(x-3)),ln(abs(x-3)))
   On obtient :
   [((x^2)/2+x)*ln(abs(x-3)),(-x^2-2*x)/(2*x-6)]
   On tape pour terminer l’intégration :
   A:=ibpu([((x^2)/2+x)*ln(abs(x-3)),(-x^2-2*x)/(2*x-6)],0)
   On obtient :
   (-x^2-10*x)/4-15*1/2*ln(abs(x-3))+((x^2)/2+x)*ln(abs(x-3))
   On tape :
   preval(A,-1,2)
   On obtient :
   8*ln(4)-9/4-6)
   On tape :
   normal(8*ln(4)-9/4-6))
   On obtient :
   8*ln(4)-33/4
   Donc l’aire cherchée vaut $(8*\ln(4)-33/4) cm^2$;

7.1.2  Exercice 2

On considère la fonction $f$ de $\mathbb{R}$ dans $\mathbb{R}$ définie par : $$f(x)=\frac{\exp(x)^2-\exp(x)+1}{\exp(x)^3+\exp(x)}$$

1. Montrer que pour tout $x \in \mathbb{R}$, $P(x)=x^4-2x^3+2x^2+1 \geq 1$
2. Étudier les variations de $f$ et tracer son graphe.
3. Trouver l’équation de la tangente au graphe au point d’abscisse $x=0$
4. Calculer $\displaystyle \int_0^x f(t)dt \$ puis, $\displaystyle \lim_{x->+\infty}\int_0^x f(t)dt$

Réponses

1. On tape :
   factor(x^4-2x^3+2x^2)
   On obtient :
   (x^2+-2*x+2)*x^2
   On tape :
   canonical_form(x^2-2*x+2)
   On obtient :
   (x-1)^2+1
   Donc pour tout $x \in \mathbb{R}$, $x^4-2x^3+2x^2=x^2*(x-1)^2+x^2 \geq 0$
   donc pour tout $x \in \mathbb{R}$, $P(x)=x^4-2x^3+2x^2+1 \geq 1$
2. On tape pour calculer la valeur de la dérivée de $f$ en un point :
   normal(derive((exp(x)^2-exp(x)+1)/(exp(x)^3+exp(x)),x))
   On obtient :
   (-(exp(x))^4+2*(exp(x))^3-2*(exp(x))^2-1)/ ((exp(x))^5+2*(exp(x))^3+exp(x))

   Le numérateur est négatif car il est égal à $-P(\exp(x))$ et le dénominateur est strictement positif car il est égal à une somme de termes strictement positifs. La fonction $f$ est donc décroissante.
   Pour chercher la limite de $f$ en $+\infty$, on tape :

   limit((exp(x)^2-exp(x)+1)/(exp(x)^3+exp(x)),x=+infinity)

   On obtient :

   0

   Pour chercher la limite de $f$ en $-\infty$, on tape :

   limit((exp(x)^2-exp(x)+1)/(exp(x)^3+exp(x)),x=-infinity)

   On obtient :

   infinity

   Pour tracer le graphe de $f$, on tape :

   plotfunc(((exp(x))^2-exp(x)+1)/((exp(x))^3+exp(x)),x)

   On obtient le graphe de $f$.

3. On définit la fonction $f$, on tape :
   f(x):=(exp(x)^2-exp(x)+1)/(exp(x)^3+exp(x))
   On calcule $f(0)$, on tape :
   f(0)
   On obtient $$\frac{1}{2}$$ On définit la fonction $df$ comme étant la dérivée de $f$, on tape :
   df:=unapply(normal(diff(f(x),x)),x)
   On calcule $df(0)$, on tape :
   df(0)
   On obtient : $$-\frac{1}{2}$$ L’équation de la tangente au point d’abscisse $0$ est donc :
   $y=df(0)*x+f(0)$ c’est à dire $\displaystyle y=-\frac{1}{2}x+\frac{1}{2}$.
   ou encore on tape :
   equation(tangent(plotfunc(f(x)),0),[x,y])
   On obtient :
   y=(1/-2*x+1/2)y=(1/-2*x+1/2)
4. On calcule l’intégrale : $\displaystyle \int_0^x f(t)dt$
   On tape :
   int(f(t),t,0,x)
   On obtient :
   (ln((exp(x))^2+1)*exp(x)+(-(2*x))*exp(x)+2*exp(x)-2)* 1/2/exp(x)-1/2*ln(2)
   Puis on calcule : $\displaystyle \lim_{x->+\infty}\int_0^x f(t)dt$, on tape :
   limit((ln((exp(x))^2+1)*exp(x)+(-(2*x))*exp(x)+2*exp(x)-2) *1/2/exp(x)-1/2*ln(2),x=+infinity)
   On obtient :
   -1/2*ln(2)+1

7.2  Calcul de primitives (niveau début université)

1. Calculer $$\int_1^2\frac{1}{x^3+1}dx$$ Réponse :
   On tape :
   int(1/(x^3+1),x,1,2)
   On obtient apres simplification (en utilisant normal}
   (sqrt(3)*ln(2)+pi)*1/3/sqrt(3)
   Pour vérifier, on tape :
   partfrac(1/(1+t^3))
   On obtient :
   1/((t+1)*3)+(-1/3*t+2/3)/(t^2-t+1)
   Puis on intègre chaque terme séparément...
2. Décomposer, sur $\mathbb{R}$, en éléments simples : $\displaystyle \frac{t^2}{1-t^4}$.
   Calculer $\displaystyle \int \frac{t^2}{1-t^4}dt\$ et $\displaystyle\int \frac{\sin(x)^2}{\cos(2x)}dx$
   Réponse :
   On tape :
   partfrac(t^2/(1-t^4))
   On obtient :
   -1/2/(t^2+1)+1/(4*(t+1))-1/4/(t-1)
   On tape :
   int(-1/2/(t^2+1)+1/(4*(t+1))-1/4/(t-1),t)
   ou on tape :
   int(t^2/(1-t^4),t)
   On obtient :
   1/(-2*atan(t))+1/(4*ln(abs(t+1)))+1/(-4*ln(abs(t-1)))
   On tape :
   normal(int(sin(x)^2/cos(2*x),x))
   On obtient :
   -1/2*x-1/-4*ln(abs((tan(1/2*x))^2-2*tan(1/2*x)-1))- 1/4*ln(abs((tan(1/2*x))^2+2*tan(1/2*x)-1))
   Ou on tape en linéarisant avant d’intégrer :
   normal(int(tlin(sin(x)^2/cos(2*x))))
   On obtient :
   1/4*ln(abs(tan(x)+1))+1/-4*ln(abs(tan(x)-1))+1/-2*x
   Ou encore on veut faire le changement de variable $\tan(x)=t$ et on tape pour avoir l’expression en fonction de la tangente, avant d’intégrer :
   trigtan(texpand(sin(x)^2/cos(2x)))
   On obtient :
   (-((tan(x))^2))/((tan(x))^2-1)
   On fait le changement de variable $x=$atan$(t)$ on tape :
   subst('integrate(-tan(x)^2/(tan(x)^2-1),x)',x=atan(t))
   ou on tape
   subst(Int(-tan(x)^2/(tan(x)^2-1),x),x=atan(t))
   On obtient
   integrate((-(t^2))/((1+t^2)*(t^2-1)),t)
   Soit, le remplacant $t$ par $\tan(x)$ :
   1/-2*atan(tan(x))+1/4*ln(abs(tan(x)+1))+1/-4*ln(abs(tan(x)-1))
3. Calculer $\displaystyle\int \frac{1}{t^2}dt,\$ $\displaystyle\int \frac{1}{t(t^2+1)}dt,\$ et $\displaystyle\int \frac{t^2-t+1}{t^4+t^2}dt$
   Réponse :
   On tape :
   int(1/t^2,t)
   On obtient :
   1/(-t)
   On tape :
   int(1/(t*(t^2+1)),t)
   On obtient :
   1/-2*ln(t^2+1)+1/2*ln((abs(t))^2)
   On tape :
   int((t^2-t+1)/(t^2+t^4),t)
   On obtient :
   1/2*ln(t^2+1)-ln(abs(t))+(-t+1)/(-t)

7.3  Dévelopements limités

1. Donner un développement limité à l’ordre 7 au voisinage de $x=0$ de : $$\sin(\sinh(x))-\sinh(\sin(x))$$ Réponse :
   On tape :
   series(sin(sinh(x))-sinh(sin(x)),x=0,7)
   On obtient:
   1/-45*x^7+x^8*order_size(x)
2. Donner un développement limité à l’ordre 4 au voisinage de $x=0$ de : $$\frac{\ln(\cos(x))}{\exp(x+x^2)}$$ Réponse :
   On tape :
   series(ln(cos(x))/exp(x+x^2),x=0,4)
   On obtient :
   1/-2*x^2+1/2*x^3+1/6*x^4+x^5*order\_size(x)
   La fonction order_size est telle que, pour tout $\alpha>0$, $x^\alpha$order_size$(x)$ tend vers 0 quand $x$ tend vers 0

7.4  Équations différentielles

1. Trouver les solutions de l’équation différentielle : $$x(x^2-1)y'+2y=0$$ Réponse :
   On tape :
   desolve(x*(x^2-1)*y'+2*y=0,y)
   On obtient :
   (c\_0*x^2)/(x^2-1)
2. Trouver les solutions de l’équation différentielle : $$x(x^2-1)y'+2y=x^2$$ Réponse :
   On tape :
   desolve(x*(x^2-1)*y'+2*y=x^2,y)
   On obtient :
   ((ln(abs(x))+c\_0)*x^2)/(x^2-1)

7.5  Les matrices

1. Soit $M_a=\left[ \begin{array}{ccc} 2a-1 & a & 2a-1\\ a^2+a-2 & a^2-1 & a-1\\ a^2+a-1 & a^2+a-1 & a \end{array} \right]$
   a) Pour quelles valeurs de $a$, $M_a$ est-elle inversible ?
   Préciser son rang lorsqu’elle n’est pas inversible.
   b) Calculer l’inverse de $M_2$

   Réponse :
   On tape :

   M:=[[2a-1,a,2a-1],[a^2+a-2,a^2-1,a-1],[a^2+a-1,a^2+a-1,a]]

   On calcule le déterminant de $M$, on tape :

   det(M)

   On obtient :

   2*a^4+-2*a^3+-2*a^2+2*a

   Pour avoir l’inverse de $M$ on tape :

   inv(M)

   On obtient : $$\frac{1}{2a^4-2a^3-2a^2+2a}\left[ \begin{array}{ccc} a-1 & 2a^3+3a+1 & -2a^3+a^2+a-1\\ -a^2+1 & -2a^3+a^2+2a-1 & 2a^3-a^2-2a+1\\ a^3-2a+1 & -a^3+2a-1 & a^3-2a^2+1 \end{array} \right]$$ On tape :

   solve(2a^4-2*a^3-2*a^2+2*a,a)

   On obtient :

   [-1,0,1]

   Donc la matrice est inversible si $a \not\in [-1,0,1]$
   Ou on tape :

   factor(2a^4-2*a^3-2*a^2+2*a)

   On obtient :

   2*(a+1)*a*(a-1)^2

   On tape :

   rank(subst(M,a,-1))

   On obtient :

   2

   On tape :

   rank(subst(M,a,0))

   On obtient :

   2

   On tape :

   rank(subst(M,a,1))

   On obtient :

   1

   On tape :

   inv(subst(M,a,2))

   On obtient : $A=\frac{1}{12}\left[ \begin{array}{ccc} 1 & 11 & -7\\ -3 & -9 & 9\\ 5 & -5 & 1 \end{array} \right]$
   Remarque : pour éviter de faire des substitutions on peut définir la matrice $M$ comme une fonction de $a$, il faut alors écrire :

   M(a):={[[2a-1,a,2a-1],[a^2+a-2,a^2-1,a-1],[a^2+a-1,a^2+a-1,a]]}

   surtout ne pas oublier { et }.
   On peut alors taper : inv(M(2)).

2. Soit $A=\left[ \begin{array}{ccc} 1 & 1 & a\\ 1 & a & 1\\ a & 1 & 1 \end{array} \right]$
   Pour quelles valeurs de $a$, $A$ est-elle diagonalisable ?

   Réponse :
   On tape :

   A:=[[1,1,a],[1,a,1],[a,1,1]]

   Pour avoir les valeurs propres de $A$ on tape :

   egvl(A)

   On obtient : $${\tt \left[ \begin{array}{ccc} -a+1 & 0 & 0\\ 0 & a+2 & 0\\ 0 & 0 & a-1 \end{array} \right] }$$ ce qui s’écrit :

   [[-a+1,0,0],[0,a+2,0],[0,0,a-1]]

   Si $a \neq 1$ il y a 3 valeurs propres distinctes $-a+1,a+2,a-1$ et
   si $a=1$ il y a une valeur propre double ($\lambda=0$) et une valeur propre simple ($\lambda=3$).
   Puis on cherche la matrice de passage, on tape :

   egv(A)

   On obtient : $${\tt \left[ \begin{array}{rrr} -1 & 1 & 1\\ 0 & 1 & -2\\ -1 & 1 & 1 \end{array} \right] }$$ ce qui s’écrit :

   [[1,1,1],[0,1,-2],[-1,1,1]]

   les vecteurs propres sont les colonnes de cette matrice.
   Ou on tape pour avoir directement les deux informations, matrice de passage et réduite de Jordan :

   jordan(A)

   On obtient une liste de deux matrices $[P,B]$ ($P$ est la matrice de passage et $B=P^{-1}AP$) : $${\tt \left[ \left[ \begin{array}{rrr} -1 & 1 & 1\\ 0 & 1 & -2\\ -1 & 1 & 1 \end{array} \right] \left[\begin{array}{ccc} -a+1 & 0 & 0\\ 0 & a+2 & 0\\ 0 & 0 & a-1 \end{array} \right] \right]}$$ ce qui s’écrit :

   [[[1,1,1],[0,1,-2],[-1,1,1]],[[-a+1,0,0],[0,a+2,0],[0,0,a-1]]]

   On remarque qu’en faisant : a:=1 puis jordan(A)
   les valeurs propres doubles sont regroupées et on obtient : $${\tt \left[ \left[ \begin{array}{rrr} 1 & -3 & 0\\ 1 & 0 & -3\\ 1 & 3 & 3 \end{array} \right] \left[\begin{array}{ccc} 3 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array} \right] \right]}$$
   ce qui s’écrit :

   [[[1,-3,0],[1,0,-3],[1,3,3]],[[3,0,0],[0,0,0],[0,0,0]]]

   $A$ est donc diagonalisable quelque soit $a$ et $B=P^{-1}AP$.

8  Vrai ou Faux ? (d’un point de vue informatique)