
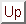



suivant: Examples of representations of
monter: Floating point representation.
précédent: Digits
Table des matières
Index
A real is represented by a floating number d, that is
d = 2
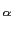
*(1 +
m), 0 <
m < 1, -2
10 <
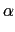
< 2
10
If
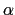 > 1 - 210, then
m
> 1 - 210, then
m 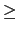 1/2, and d is
a normalized floating point number, otherwise
d is denormalized (
1/2, and d is
a normalized floating point number, otherwise
d is denormalized (
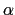 = 1 - 210). The special exponent 210
is used to represent plus or minus infinity and NaN (Not a Number).
A hardware float is made of 64 bits:
= 1 - 210). The special exponent 210
is used to represent plus or minus infinity and NaN (Not a Number).
A hardware float is made of 64 bits:
- the first bit is for the sign of d (0 for '+' and 1 for '-')
- the 11 following bits represents the exponent, more precisely
if
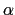 denotes the integer from the 11 bits,
the exponent is
denotes the integer from the 11 bits,
the exponent is
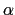 +210 - 1,
+210 - 1,
- the 52 last bits codes the mantissa m, more precisely if
M denotes the integer from the 52 bits, then
m = 1/2 + M/253 for normalized floats and
m = M/253 for
denormalized floats.
Examples of representations of the exponent:
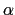 = 0 is coded by 011 1111 1111
= 0 is coded by 011 1111 1111
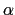 = 1 is coded by 100 0000 0000
= 1 is coded by 100 0000 0000
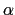 = 4 is coded by 100 0000 0011
= 4 is coded by 100 0000 0011
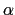 = 5 is coded by 100 0000 0100
= 5 is coded by 100 0000 0100
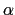 = - 1 is coded by 011 1111 1110
= - 1 is coded by 011 1111 1110
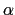 = - 4 is coded by 011 1111 1011
= - 4 is coded by 011 1111 1011
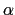 = - 5 is coded by 011 1111 1010
= - 5 is coded by 011 1111 1010
-
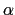 = 210 is coded by 111 1111 1111
= 210 is coded by 111 1111 1111
-
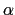 = 2-10 - 1 is coded by 000 0000 000
= 2-10 - 1 is coded by 000 0000 000
Remark:
2-52 = 0.2220446049250313e - 15




suivant: Examples of representations of
monter: Floating point representation.
précédent: Digits
Table des matières
Index
giac documentation written by Renée De Graeve and Bernard Parisse