Animation of a sequence of graphic objects : animation

animation animates the representation of a sequence of graphic objects with a given display time. The sequence of objects depends most of the time of a parameter and is defined using the seq command but it is not mandatory.
animation takes as argument the sequence of graphic objects.
To define a sequence of graphic objects with seq, enter the definition of the graphic object (depending on the parameter), the parameter name, it's minimum value, it's maximum value maximum and optionnaly a step value.
Input :

animation(seq(plotfunc(cos(a*x),x),a,0,10))

Output :

The sequence of the curves defined by y = cos(ax), for a = 0, 1, 2..10

Input :

animation(seq(plotfunc(cos(a*x),x),a,0,10,0.5))
or
animation(seq(plotfunc(cos(a*x),x),a=0..10,0.5))

Output :

The sequence of the curves defined by y = cos(ax), for a = 0, 0.5, 1, 1.5..10

Input :

animation(seq(plotfunc([cos(a*x),sin(a*x)],x=0..2*pi/a), a,1,10))

Output :

The sequence of two curves defined by y = cos(ax) and y = sin(ax), for a = 1..10 and for x = 0..2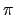$\pi$/a

Input :

animation(seq(plotparam([cos(a*t),sin(a*t)], t=0..2*pi),a,1,10))

Output :

The sequence of the parametric curves defined by x = cos(at) and y = sin(at), for a = 1..10 and for t = 0..2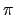$\pi$

Input :

animation(seq(plotparam([sin(t),sin(a*t)], t,0,2*pi,tstep=0.01),a,1,10))

Output :

The sequence of the parametric curves defined by x = sin(t), y = sin(at), for a = 0..10 and t = 0..2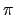$\pi$

Input :

animation(seq(plotpolar(1-a*0.01*t^2, t,0,5*pi,tstep=0.01),a,1,10))

Output :

The sequence of the polar curves defined by 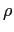$\rho$ = 1 - a*0.01*t², for a = 0..10 and t = 0..5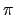$\pi$

Input :

plotfield(sin(x*y),[x,y]); animation(seq(plotode(sin(x*y),[x,y],[0,a]),a,-4,4,0.5))

Output :

The tangent field of y'=sin(xy) and the sequence of the integral curves crossing through the point (0, a) for a=-4,-3.5...3.5,4

Input :

animation(seq(display(square(0,1+i*a),filled),a,-5,5))

Output :

The sequence of the squares defined by the points 0 and 1+i*a for a = - 5..5

Input :

animation(seq(droite([0,0,0],[1,1,a]),a,-5,5))

Output :

The sequence of the lines defined by the points [0,0,0] and [1,1,a] for a = - 5..5

Input :

animation(seq(plotfunc(x^2-y^a,[x,y]),a=1..3))

Output :

The sequence of the "3D" surface defined by x² - y^a, for a = 1..3 with rainbow colors

Input :

animation(seq(plotfunc((x+i*y)^a,[x,y], display=filled),a=1..10)

Output :

The sequence of the "4D" surfaces defined by (x + i*y)^a, for a = 0..10 with rainbow colors

Remark We may also define the sequence with a program, for example if we want to draw the segments of length 1,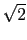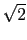$\sqrt{2}$...$\sqrt{2}$ 0 constructed with a right triangle of side 1 and the previous segment (note that there is a c:=evalf(..) statement to force approx. evaluation otherwise the computing time would be too long) :

seg(n):={
 local a,b,c,j,aa,bb,L;
 a:=1;
 b:=1;
 L:=[point(1)];
 for(j:=1;j<=n;j++){
  L:=append(L,point(a+i*b));
  c:=evalf(sqrt(a^2+b^2));
  aa:=a;
  bb:=b;
  a:=aa-bb/c;
  b:=bb+aa/c;
 }
 L;
}

Then input :

animation(seg(20))

We see, each point, one to one with a display time that depends of the animate value in cfg.
Or :

L:=seg(20); s:=segment(0,L[k])$(k=0..20)

We see 21 segments.
Then, input :

animation(s)

We see, each segment, one to one with a display time that depends of the animate value in cfg.