MPHELL  4.0.0
Weiestrass elliptic curves

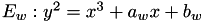Let $ E_w: y^2 = x^3 + a_wx + b_w $ be a Weierstrass elliptic curve under affine coordinates. Under Projective coordinates 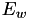$ E_w $ becomes 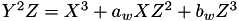$ Y^2Z = X^3 + a_wXZ^2 + b_wZ^3 $. The triple (X, Y, Z) represents the affine point (X / Z, Y / Z)

Under Jacobian coordinates 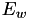$ E_w $ becomes 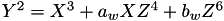$ Y^2 = X^3 + a_wXZ^4 + b_wZ^6 $. The triple (X, Y, Z) represents the affine point (X / Z^2, Y / Z^3).

The main references for the formulas are

  1. [Ber01] A software implementation of NISTP 224 by Bernstein, Daniel J. in Elliptic Curve Cryptography (ECC) 2001. University of Waterloo, Ontario available here at this page https://cr.yp.to/talks.html
  2. [BL07] Faster addition and doubling on elliptic curves by Bernstein, Daniel J., Lange, Tanja in : International Conference on the Theory and Application of Cryptology and Information Security. Springer, Berlin, Heidelberg, 2007. p. 29-50. viewable at this website https://link.springer.com/
  3. [CMO98] Efficient elliptic curve exponentiation using mixed coordinates by Cohen, Henri, Miyaji Atsuko , and On, Takatoshi. published in International Conference on the Theory and Application of Cryptology and Information Security. Springer, Berlin, Heidelberg, 1998 viewable at this website https://link.springer.com/
  4. [GJM10] Co-Z Addition Formulæ and Binary Ladders on Elliptic Curves by Goundar, Raveen R., Joye, Marc and Miyaji Atsuko in : International Workshop on Cryptographic Hardware and Embedded Systems. Springer, Berlin, Heidelberg, 2010. p. 65-79. viewable at this website https://link.springer.com/

Projective Coordinates

Let

  1. P1 = (X1,Y1,Z1)
  2. P2 = (X2,Y2,Z2)

Dedicated Addition

This formula is from [CMO98] and referenced as the "Eliminating common subexpressions from 1998 Cohen/Miyaji/Ono" in the website https://hyperelliptic.org/ .

The point P3 = (X3,Y3,Z3) = P1 + P2 is given by

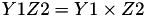
  1. $ Y1Z2 = Y1 \times Z2 $
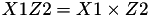
  2. $ X1Z2 = X1 \times Z2 $
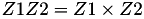
  3. $ Z1Z2 = Z1 \times Z2 $
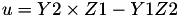
  4. $ u = Y2 \times Z1 - Y1Z2 $
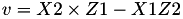
  5. $ v = X2 \times Z1 - X1Z2 $
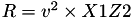
  6. $ R = v^2 \times X1Z2 $
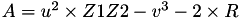
  7. $ A = u^2 \times Z1Z2 - v^3 - 2 \times R $
  8. $ X3 = v \times A $
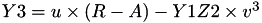
  9. $ Y3 = u \times (R - A) - Y1Z2 \times v^3 $
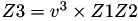
  10. $ Z3 = v^3 \times Z1Z2 $

using 12 multiplications, 2 squares and 6 additions and 1 times 2.

Dedicated Doubling

This formula is referenced as the "dbl-2007-bl" from [BL07] in the website https://hyperelliptic.org/ .

The point P3 = (X3,Y3,Z3) = 2P1 is given by

  1. $ w = a_w \times Z1^2 + 3 \times X1^2 $
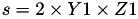
  2. $ s = 2 \times Y1 \times Z1 $
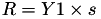
  3. $ R = Y1 \times s $
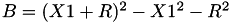
  4. $ B = (X1 + R)^2 - X1^2 - R^2 $
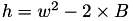
  5. $ h = w^2 - 2 \times B $
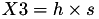
  6. $ X3 = h \times s $
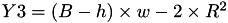
  7. $ Y3 = (B - h) \times w - 2 \times R^2 $
  8. $ Z3 = s^3 $

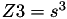
using 5 multiplications + 6 squares + 7 additions + 3 times 2 + 1 times 3 + 1 times a:

if 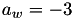$ a_w = -3 $ we use the formula "dbl-2007-bl-2" from [BL07] in the website https://hyperelliptic.org/ .

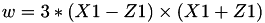
  1. $ w = 3*(X1-Z1) \times (X1+Z1) $
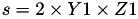
  2. $ s = 2 \times Y1 \times Z1 $
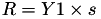
  3. $ R = Y1 \times s $
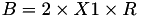
  4. $ B = 2 \times X1 \times R $
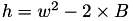
  5. $ h = w^2 - 2 \times B $
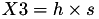
  6. $ X3 = h \times s $
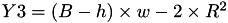
  7. $ Y3 = (B - h) \times w - 2 \times R^2 $
  8. $ Z3 = s^3 $

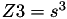
using 7 multiplications + 3 squares + 5 additions + 4 times 2 + 1 times 3

Unified Addition

This formula is referenced as the "add-2007-bl" from [BL07] in the website https://hyperelliptic.org/ .

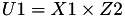
  1. $ U1 = X1 \times Z2 $
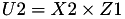
  2. $ U2 = X2 \times Z1 $
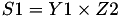
  3. $ S1 = Y1 \times Z2 $
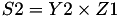
  4. $ S2 = Y2 \times Z1 $
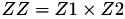
  5. $ ZZ = Z1 \times Z2 $
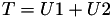
  6. $ T = U1+U2 $
  7. $ TT = T2 $
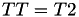
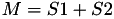
  8. $ M = S1+S2 $
  9. $ R = TT-U1 \times U2+a \times ZZ^2 $
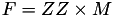
  10. $ F = ZZ \times M $
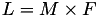
  11. $ L = M \times F $
  12. $ LL = L2 $
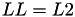
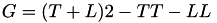
  13. $ G = (T+L) 2-TT-LL $
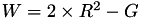
  14. $ W = 2 \times R^2-G $
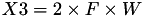
  15. $ X3 = 2 \times F \times W $
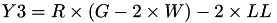
  16. $ Y3 = R \times (G-2 \times W)-2 \times LL $
  17. $ Z3 = 4 \times F \times F^2 $

using 11 multiplications + 6 squares + 1*a + 10 additions + 4 times 2 + 1 times 4.

Jacobian Coordinates

Addition

This formula is an adaptation from the one used by ipp-crypto , the beginning is the same than 2007 Bernstein/Lange" from [BL07] but using less addition.

The point P3 = (X3,Y3,Z3) = P1 + P2 is given by

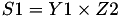
  1. $ S1 = Y1 \times Z2 $
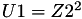
  2. $ U1 = Z2^2 $
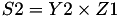
  3. $ S2 = Y2 \times Z1 $
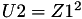
  4. $ U2 = Z1^2 $
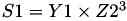
  5. $ S1 = Y1 \times Z2^3 $
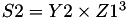
  6. $ S2 = Y2 \times Z1^3 $
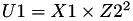
  7. $ U1 = X1 \times Z2^2 $
  8. $ U2 = X2 \times Z1^2 $
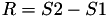
  9. $ R = S2 - S1 $
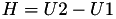
  10. $ H = U2 - U1 $
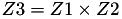
  11. $ Z3 = Z1 \times Z2 $
  12. $ U2 = H^2 $
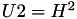
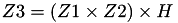
  13. $ Z3 = (Z1 \times Z2) \times H $
  14. $ S2 = R^2 $
  15. $ H = H^3 $
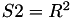
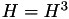
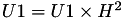
  16. $ U1 = U1 \times H^2 $
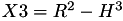
  17. $ X3 = R^2 - H^3 $
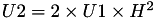
  18. $ U2 = 2 \times U1 \times H^2 $
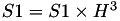
  19. $ S1 = S1 \times H^3 $
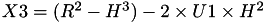
  20. $ X3 = (R^2 - H^3) - 2 \times U1 \times H^2 $
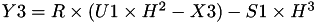
  21. $ Y3 = R \times (U1 \times H^2 - X3) - S1 \times H^3 $

using 12 multiplications + 4 squares + 6 additions + 1 times 2

Doubling

This formula is an adaptation from the one used by ipp-crypto , it uses less additions than the ones referenced by "2007 Bernstein/Lange" and "2001 Bernstein"

The point P3 = (X3,Y3,Z3) = 2P1 is given by

  1. $ S = 2*Y $
  2. $ U = Z^2 $
  3. $ M = 2*Y^2 $
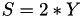
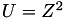
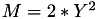
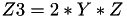
  4. $ Z3 = 2*Y*Z $
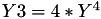
  5. $ Y3 = 4*Y^4 $
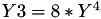
  6. $ Y3 = 8*Y^4 $
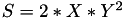
  7. $ S = 2*X*Y^2 $
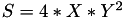
  8. $ S = 4*X*Y^2 $
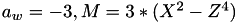
    • If $ a_w = -3, M = 3*(X^2-Z^4) $
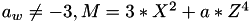
    • If $ a_w \neq -3, M = 3*X^2+a*Z^4 $
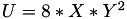
  10. $ U = 8*X*Y^2 $
  11. $ X3 = M^2 $
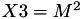
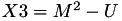
  12. $ X3 = M^2 - U $
  13. $ S = 4*X*Y^2-X3 $
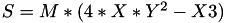
  14. $ S = M*(4*X*Y^2-X3) $
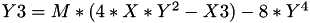
  15. $ Y3 = M*(4*X*Y^2-X3) - 8*Y^4 $

using 5 multiplications + 3 squares + 5 additions + 4 times 2 + 1 times 3 when 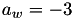$ a_w = -3 $ and

7 multiplications + 3 squares + 4 additions + 4 times 2 + 1 times 3 when 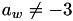$ a_w \neq -3 $

Jacobian Coordinates using Co-Z arithmetic

When elliptic curve points share the same z-coordinate, a faster arithmetic (Co-Z) can be used.

All the algorithm of Co-Z arithmetic implemented in MPHELL can be found in the paper [GJM10] and all those algorithms take in inputs points with the same Z coordinate.

Addition

The points P3 = (X3,Y3,Z3) = P1 + P2 and update the point P1 such that Z1 = Z3.

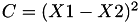
  1. $ C = (X1 - X2)^2 $
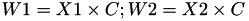
  2. $ W1 = X1 \times C; W2 = X2 \times C $
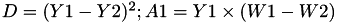
  3. $ D = (Y1 - Y2)^2; A1 = Y1 \times (W1 - W2) $
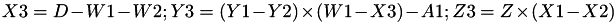
  4. $ X3 = D - W1 - W2; Y3 = (Y1 - Y2) \times (W1 - X3) - A1; Z3 = Z \times (X1 - X2) $
  5. $ X1 = W1; Y1 = A1; Z1 = Z3 $

This operation is called ZADDU and costs 5 multiplications + 2 squares + 7 additions and can be found precisely in [GJM10,§2.2 algorithm 1].

Conjugate addition

The point P3 = (X3,Y3,Z3) = P1 + P2 and the point P4 = (X4,Y4,Z4) = P1-P2 such that Z4 = Z3.

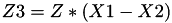
  1. $ Z3 = Z * (X1 - X2) $
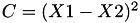
  2. $ C = (X1 -X2)^2 $
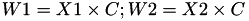
  3. $ W1 = X1 \times C ; W2 = X2 \times C$
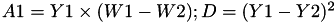
  4. $ A1 = Y1 \times (W1 - W2); D = (Y1 - Y2)^2 $
  5. $ X3 = D - W1 - W2 ;Y3 = (Y1 - Y2) \times (W1 - X3) - A1 $
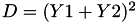
  6. $ D = (Y1 + Y2)^2 $
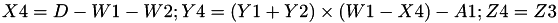
  7. $ X4 = D - W1 - W2; Y4 = (Y1 + Y2) \times (W1 - X4) - A1; Z4 = Z3 $

This operation is called ZADDC and costs 6 multiplications + 3 squares + 11 additions and can be found in [GJM, §4 algorithm 6].

Doubling

The points P3 = (X3,Y3,Z3) = 2*P1 and the point P4 such that P1 = P4 and Z4 = Z3 and assume that P1->z==1.

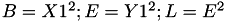
  1. $ B = X1^2; E = Y1^2; L = E^2 $
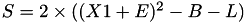
  2. $ S = 2 \times ((X1 + E)^2 - B - L) $
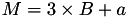
  3. $ M = 3 \times B + a $
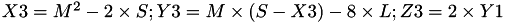
  4. $ X3 = M^2 - 2 \times S; Y3 = M \times (S - X3) - 8 \times L; Z3 = 2 \times Y1 $
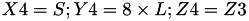
  5. $ X4 = S; Y4 = 8 \times L; Z4 = Z3 $

This operation is called DBLU and costs 1 multiplication + 5 squares + 6 additions + 3 times 2 + 1 times 3 +1 times 8 and can be found in [GJM10, §4.3]

Combined Double-Add

The points P3 = (X3,Y3,Z3) = 2 P1 + P2 and update P2 such that Z2 = Z3.

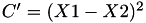
  1. $ C' = (X1-X2)^2 $
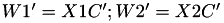
  2. $ W1' = X1C'; W2' = X2C' $
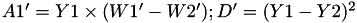
  3. $ A1' = Y1 \times (W1'-W2'); D' = (Y1-Y2)^2 $
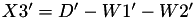
  4. $ X3' = D' - W1' -W2' $
  5. $ C = (X3' - W1')^2 $
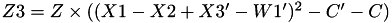
  6. $ Z3 =Z \times ((X1-X2+X3'-W1')^2-C'-C) $
  7. $ Y3' = [(Y1-Y2) - (X3'-W1')]^2 - D' - C - 2 \times A1' $
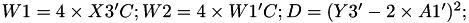
  8. $ W1 = 4 \times X3'C; W2 = 4 \times W1'C; D = (Y3' - 2 \times A1')^2; $
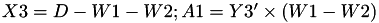
  9. $ X3 = D - W1 - W2; A1 = Y3' \times (W1-W2) $
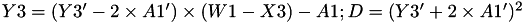
  10. $ Y3 = (Y3' - 2 \times A1') \times (W1 - X3) - A1; D = (Y3' + 2 \times A1')^2 $
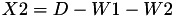
  11. $ X2 = D - W1 - W2 $
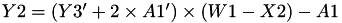
  12. $ Y2 = (Y3'+ 2 \times A1') \times (W1-X2)-A1 $

  13. $ Z2 = Z3 $

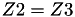
This operation is called ZDAU and costs 9 multiplications + 7 squares + 22 additions + 1 time 2 + 1 times 4 and can be found in [GJM, §4.4 algorithm 9].

Jacobian Coordinates, fast unified multiplication used in MPHELL

The unified multiplication currently used in MPHELL can be found in the paper: Speeding up Elliptic Curve Scalar Multiplicationwithout Precomputation.

By Kwang Ho Kim, Junyop Choe, Song Yun Kim, and Namsu Kim and Sekung Hong.

Generated by   doxygen 1.8.15