 |
MPHELL
4.0.0
|
 |
MPHELL
4.0.0
|
Jacobi Quartics elliptic curves are elliptic curves given by the equation
Let 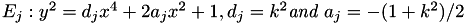 be a Jacobi Quartic elliptic curve under affine coordinates.
be a Jacobi Quartic elliptic curve under affine coordinates.
Under projective coordinates 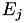 becomes
becomes 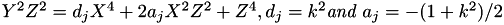 . The triplet (X, Y, Z) represents the affine point (X / Z, Y / Z).
. The triplet (X, Y, Z) represents the affine point (X / Z, Y / Z).
Under extended homogenous projective coordinates 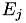 becomes
becomes 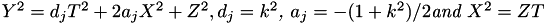 . The quadruplet (X, Y, T, Z) represents the affine point (X / Z, Y / Z) with
. The quadruplet (X, Y, T, Z) represents the affine point (X / Z, Y / Z) with 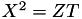 .
.
An elliptic curve 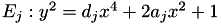 with this equation is called an extended jacobi quartic elliptic curve, in MPHELL we work only in this case with
with this equation is called an extended jacobi quartic elliptic curve, in MPHELL we work only in this case with 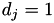 in the extended homogeneous projective coordinates.
in the extended homogeneous projective coordinates.
These formulas are derived from the paper [HKCD09] "Jacobi Quartic Curves Revisited" written by Huseyin Hisil, Kenneth Koon-Ho Wong, Gary Carter and Ed Dawson published in Australasian Conference on Information Security and Privacy 2009 (pp. 452-468). Springer, Berlin, Heidelberg viewable at this adress : https://link.springer.com/ .
Let 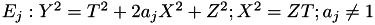 a Jacobi Quartic elliptic curve under extended homogeneous projective coordinates.
a Jacobi Quartic elliptic curve under extended homogeneous projective coordinates.
Under affine coordinates 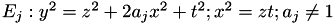 becomes
becomes 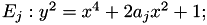 .
.
Let
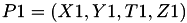
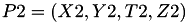
The point 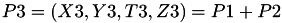 is given by
is given by
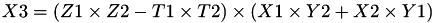
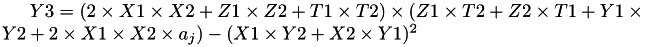
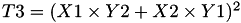
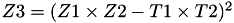
using 8 multiplications, 2 squares and 1 times a 13 additions and 1 times 2.
It is noticeable that this is a simplified formula of a more general formula for extended jacobi quartic.
More details are in [HKCD09,§4.3,B].
With use the unified addition:
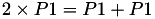
We use the unified addition formulae because it is in the general case the fastest addition in extended homogeneous projective coordinates.
Let
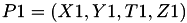
The point 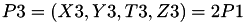 is given by
is given by
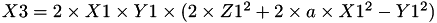
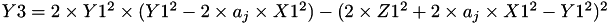
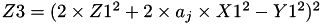
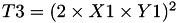
using 3 multiplications, 5 squares, 1 times a, 13 additions and 4 times 2
More details are in [HKCD09,§3.1].
 1.8.15
1.8.15