Introduction
The MPHELL library implements Elliptic Curve arithmetic:
-
Points addition
-
Points substraction
-
Points doubling
-
Points multiplication
-
Test if a point belong to a given curve
We provide a Simple Power Analysis (SPA) resistant multiplication using unified addition (and COZ arithmetic for Weierstrass curves).
Some dedicated addition / doubling are also provided to improve performances when security is not required.
Available curve types:
-
WEIERSTRASS,
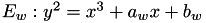
-
JACOBI_QUARTIC,
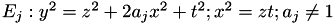
-
EDWARDS,
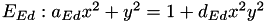
Possible conversion:
-
WEIERSTRASS -> JACOBI_QUARTIC, but you need
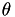 such that
such that 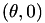 is a 2-torsion point on the Weierstrass elliptic curve.
is a 2-torsion point on the Weierstrass elliptic curve.
-
JACOBI_QUARTIC -> WEIERSTRASS
-
TWISTED EDWARDS -> WEIERSTRASS
-
WEIERSTRASS -> TWISTED EDWARDS, but you need
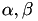 such that
such that 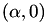 is a 2-torsion point on the Weierstrass elliptic curve and that
is a 2-torsion point on the Weierstrass elliptic curve and that 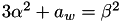 .
.
Available coordinates for Weierstrass elliptic curve:
-
PROJECTIVE: (X,Y,Z) matching the affine point (x,y) where x=X/Z, y=Y/Z, the point at infinity is (0,1,0)
-
JACOBIAN: (X,Y,Z) matching the affine point (x,y) where x=X/Z^2, y=Y/Z^3, the point at infinity is (a^2,a^3,0) with a!=0
Available coordinates for Twisted Edwards elliptic curve:
-
PROJECTIVE: (X,Y,Z) matching the affine point (x,y) where x=X/Z, y=Y/Z, the point at infinity is (0,1,0)
-
EXTENDED_EDWARDS: (X,Y,T,Z) matching the affine point (x,y) where x=X/Z, y=Y/Z, and the coordinate T should verify that T=XY/Z, the point at infinity is (0,1,0,1).
Available coordinates for extended Jacobi Quartic elliptic curve:
-
EXTENDED_HOMOGENEOUS_PROJECTIVE (X,Y,T,Z) matching the affine point (x,y) where x=X/Z, y=Y/Z and the coordinate T should verify that X^2=TZ, the point at infinity is (0,1,0,1).
Curve can be given manually giving
-
"a" and "b" coefficients for a Weierstrass Elliptic Curve
-
"a" coefficient for an extended Jacobi Quartic Elliptic Curve (with d=1)
-
"a" and "b" (instead of d) coefficients for a Twisted Edwards Elliptic Curve
-
G, base point on the curve
-
n, the order of G
-
h, the cofactor of n
Some known curves are hardcoded and can be setup by their names (eg: FR_256, BRAINPOOL_512, NIST_521, ...).
This library can be used on Linux operating system (x86, 32 and 64 bits), on ARM 32 bits (tested on Raspberry Pi 2) and on microcontroller (tested on STM32F4).
Modular arithmetic
The modular (field level) arithmetic is either managed by
IPP is faster, especially for NIST curves, but for x86 only.
MbedTLS is faster on stm32 microcontroller (dedicated ASM).
When GMP or MbedTLS is used for the big number arithmetic, the field arithmetic is then build over this big number arithmetic. We can choose (at configure time) to use either a
-
Classical modular arithmetic
-
Montgomery arithmetic (default because it is faster)
Finite fields
Available finite fields are
-
FP, primary field of characteristic a prime number p
-
FP2, quadratic extension of characteristic a prime number p and order p^2. The irreduciple polynomial must me on the form (X^2 - a) where a is a non-square residue in FP.
-
FP3, cubic extension of characteristic a prime number p and order p^3. The irreduciple polynomial must me on the form (X^3 - a) where a is a non-cubic residue in FP.
Random number generation
MPHELL has a random number generation system in accordance with the "NIST Special Publication 800-90A".
Entropy
The seed (and the nonce) are extrated from one of the entropy source available in MPHELL:
-
/dev/urandom a non blocant entropy source, can be of poor quality
-
/dev/random a blocant entropy source, can be slow, consider installing HAVEGED to increase the entropy throughput
-
RDSEED instruction, available since Broadwell ("5th-generation Core" of the Intel Core processors)
Deterministic Random Bit Gerenators
Two types of DRBG are supported in MPHELL:
-
HASH-DRBG using:
-
SHA1 hash function, can be used for a security strength <= 128 bits
-
SHA256 hash function, can be used for a security strength <= 256 bits
-
CTR-DRBG using:
-
AES-128 block cipher, can be used for a security strength <= 128 bits
-
AES-192 block cipher, can be used for a security strength <= 192 bits
-
AES-256 block cipher, can be used for a security strength <= 256 bits
Default parameters
The following parameters are used by MPHELL when using its own DRBG:
-
The nonce is extracted from the entropy source of size (entropy length / 2)
-
The personalization string is NULL
-
The additional input when reseeding is NULL
-
The additional input when generating random bytes is NULL
-
The reseed interval is 2^20 = 1048576, provides only Backtracking resistance (must be 1 to provide Prediction Resistance).
Random Generator using their own entropy source
Two types of Random Generator using their own entropy source are available in MPHELL:
-
RDRAND instruction, available since Ivy Bridge ("third generation" of the Intel Core processors)
-
The stm32f4 generator, if MPHELL is running on the microcontroller
Test
The 15 tests made by the the NIST sts program, have been passed by all the combination of MPHELL entropy and DRBG availables. In order to fullfill the requirements of all the tests we used the following parameters:
-
The bitstream length n = 10^6
-
The number of bitstreams = 100
-
All the other test parameters are the default proposed by the NIST program
The DRBG (both HASH-DRBG and CTR-DRBG) are tested with the NIST vector tests while running "make check"
Temporary memory
In order to avoid multiple system calls (malloc, free, ...) we use some temporary memory stacks and some pools of already initialised field elements.
Multithreading
In order to use MPHELL in different threads you must:
-
Configure with: –enable-multithreading=yes
-
Use the MPHELL functions with a different memory stack (STACK_1, STACK_2, ...) for each thread
Requirement
-
-
GMP version 6.0.0 or higher, for big number arithmetic OR
-
IPP version 2020.0.0 or higher, for field arithmetic OR
-
MbedTLS version 2.11.0 or higher, for big number arithmetic
-
doxygen and graphviz for the documentation
Installation (on x86 architecture)
If you got MPHELL from the git repository run (require autoconf, automake, libtool): autoreconf --i
Installation with IPP
If ipp-crypto is install in /path/to/ipp-crypto (ex: /home/softs/ipp-crypto), run the commands:
-
./configure --enable-ipp --with-ipp=/path/to/ipp-crypto (ex: ./configure --enable-ipp --with-ipp=/home/softs/ipp-crypto)
-
make
-
make check
-
make install (need the root rights to install in /usr/local)
Installation with GMP if GMP is installed in /usr/ or /usr/local/
Run the classical commands:
-
./configure --enable-gmp
-
make
-
make check
-
make install (need the root rights to install in /usr/local)
Installation with GMP installed elsewhere
If GMP is install in /path/to/gmp, run the commands:
-
./configure --enable-gmp --with-gmp=/path/to/gmp
-
make
-
make check
-
make install (need the root rights to install in /usr/local)
Installation with MbedTLS if MbedTLS is installed in /usr/ or /usr/local/
Run the classical commands:
-
./configure --enable-mbedtls
-
make
-
make check
-
make install (need the root rights to install in /usr/local)
Installation with MbedTLS installed elsewhere
If GMP is install in /path/to/gmp, run the commands:
-
./configure --enable-mbedtls --with-mbedtls=/path/to/mbedtls
-
make
-
make check
-
make install (need the root rights to install in /usr/local)
Configure options
Default values are in uppercase.
-
--enable-optimisation=YES/no (Use -O3)
-
--enable-montgomery=YES/no, use Montgomery arithmetic (for GMP only).
-
--enable-multithreading=yes/NO (Allow to use STACK_1 and STACK_2 for temporary memory, for GMP only)
-
--enable-debug=yes/NO (add -g and, remove -DNDEBUG, and enable MPHELL_USE_ASSERT)
-
--enable-valgrind=yes/NO, create a target in test/ to run make check-valgrind
-
--help gives other informations (especially for external package paths)
Cross-Compilation (for STM32F4)
Toolchain
A toolchain for bare metal compilation is available here: arm-none-eabi toolchain
You can add the path of your toolchain binaries to the PATH environnement variable with: export PATH=$PATH:/path/to/toolchain/bin
MPHELL with MbedTLS (fastest)
MbedTLS provides a faster arithmetic for the STM32F4 compare to GMP. A factor 5 can be observed.
MbedTLS Cross Compilation
The sources of MbedTLS can be included in your project Makefile, and be crosscompiled with your project. These sources are in the repository Middlewares/Third_Party/ if you activated "mbedTLS" in the STM32CubeMX code generator.
MPHELL Cross Compilation
On the same scheme than MbedTLS, you can add the sources of MPHELL to your project Makefile and crosscompile it with your project. We provide here a source directory with MPHELL configured for MbedTLS to paste in your Middlewares/Third_Party/ directory.
MPHELL with GMP (slowest)
GMP is slower than MbedTLS on the STM32, but still works.
GMP Cross Compilation
-
./configure CC=arm-none-eabi-gcc CFLAGS="-nostartfiles --specs=nosys.specs -mcpu=cortex-m4" --host=arm-none-eabi --disable-assembly --prefix=your-bare-metal-gmp-location
-
make
-
make install
MPHELL Cross Compilation
-
CC=arm-none-eabi-gcc ./configure --host=arm-none-eabi --prefix=your-bare-metal-mphell-location --enable-gmp --with-gmp=your-bare-metal-gmp-location
-
make
-
make install
Used formulas for elliptic curves
Weiestrass elliptic curves
Jacobi Quartic elliptic curves
Edwards elliptic curves
Conversion between Weiestrass and Jacobi Quartic elliptic curves
Conversion between Short Weierstrass Curve Model and Twisted Edwards Curves Model
Tutorials
All tutorial can be compile with gcc mphell_tuto_fp.c \
-I/your-gmp-location/include \
-L/your-gmp-location/lib \
-lgmp \
-I/your-mphell-location \
-L/your-mphell-location/lib \
-Wl,-rpath=your-mphell-location/lib \
-lmphell \
-o tuto_fp
by replacing mphell_tuto_fp.c and tuto_fp by the tutorial you want to compile.
Field arithmetic
FP
Look at mphell_tuto_fp.c
FP2
MPHELL handle only quadratic field extension over FP, with irreducible polynomial x^2-a where a is a non square in FP
Look at mphell_tuto_fp2.c
FP3
MPHELL handle only cubic field extension over FP, with irreducible polynomial x^3-a where a is a non cubic element in FP
Look at mphell_tuto_fp3.c
Random
One time MPHELL is instantiated, MPHELL provides functions to get random elements, at
-
Number level
-
Field level (FP, FP2, FP3)
-
Curve level (Weierstrass, Jacobi quartic, Edwards)
The following tutorials are only to understand, and evaluate the underlying random process
DRBG use
Look at mphell_tuto_drbg.c
Random use
Look at mphell_tuto_random.c
Elliptic curves
Weierstrass
Look at mphell_tuto_weierstrass.c
Jacobi Quartic
Look at mphell_tuto_jacobi_quartic.c
Edwards
Look at mphell_tuto_edwards.c
ECDSA
Look at mphell_tuto_ecdsa.c or
Add -fopenmp to the compilation line (the signature verification is parallelised), verify that MPHELL was configure with "--enable-multithreading=yes" and
Look at mphell_tuto_ecdsa_fips.c
Bugs report
In case of problem using MPHELL, thanks to:
-
Configure MPHELL with the option --enable-debug=yes, then make clean, make check, make install.
-
If the make check does not work, attach a copy of test-suite.log (in test/ directory) to your email
-
If your program reveal a new bug, isolate if possible the bug and attach an easy C program to your email
-
Precise your OS (Linux are the only tested OS), and your processor specification (cat /proc/cpuinfo)
-
Send your email at mphell@univ-grenoble-alpes.fr
Benchmarks
Benchmark on x86 64 bits
The benchmarks are made on a x86_64 architecture with an Intel Core i7-4790 CPU 3.60GHz × 8.
MPHELL uses some unified operations (slower) for the signatures to make it resistant to SPA, it's not the case for the others.
MPHELL uses some dedicated operations and some precomputation technics for the verification to make it faster.
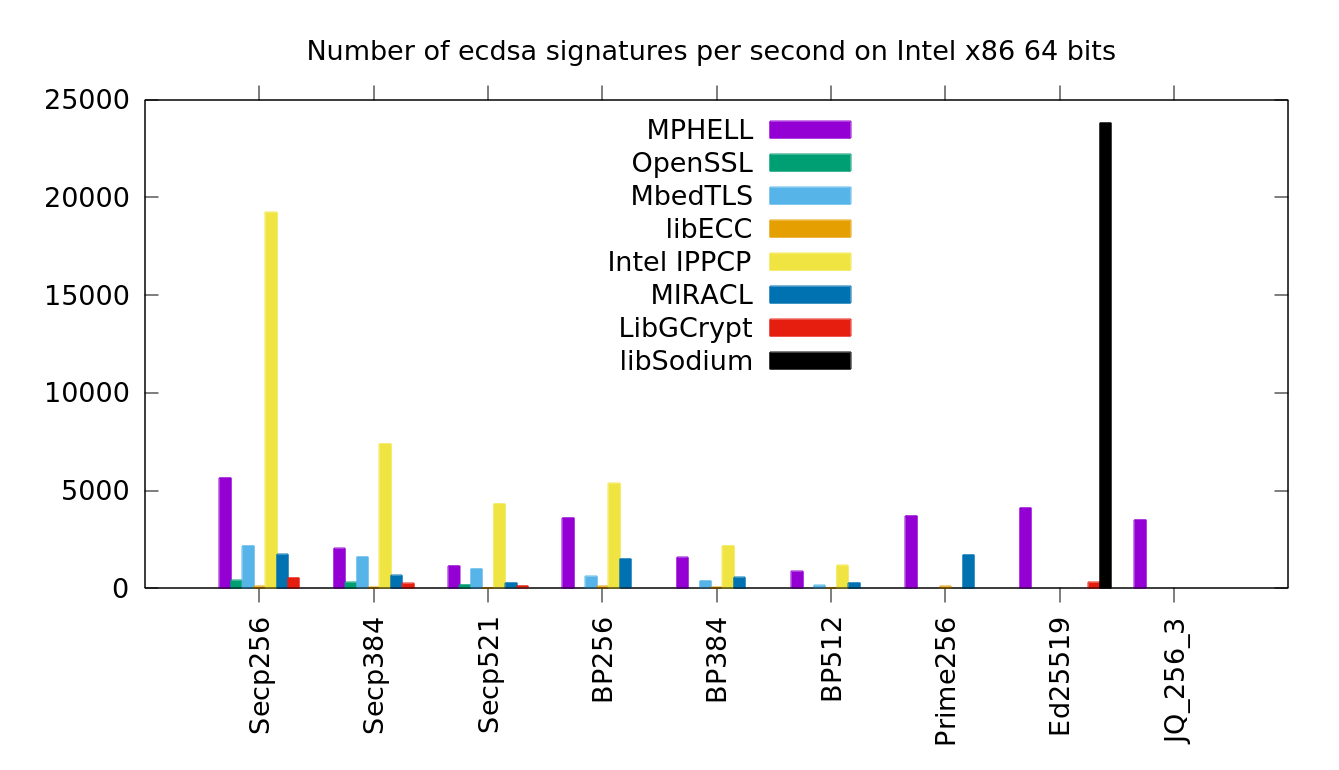
Comparison between MPHELL (using IPP) and other softs for ECDSA signatures
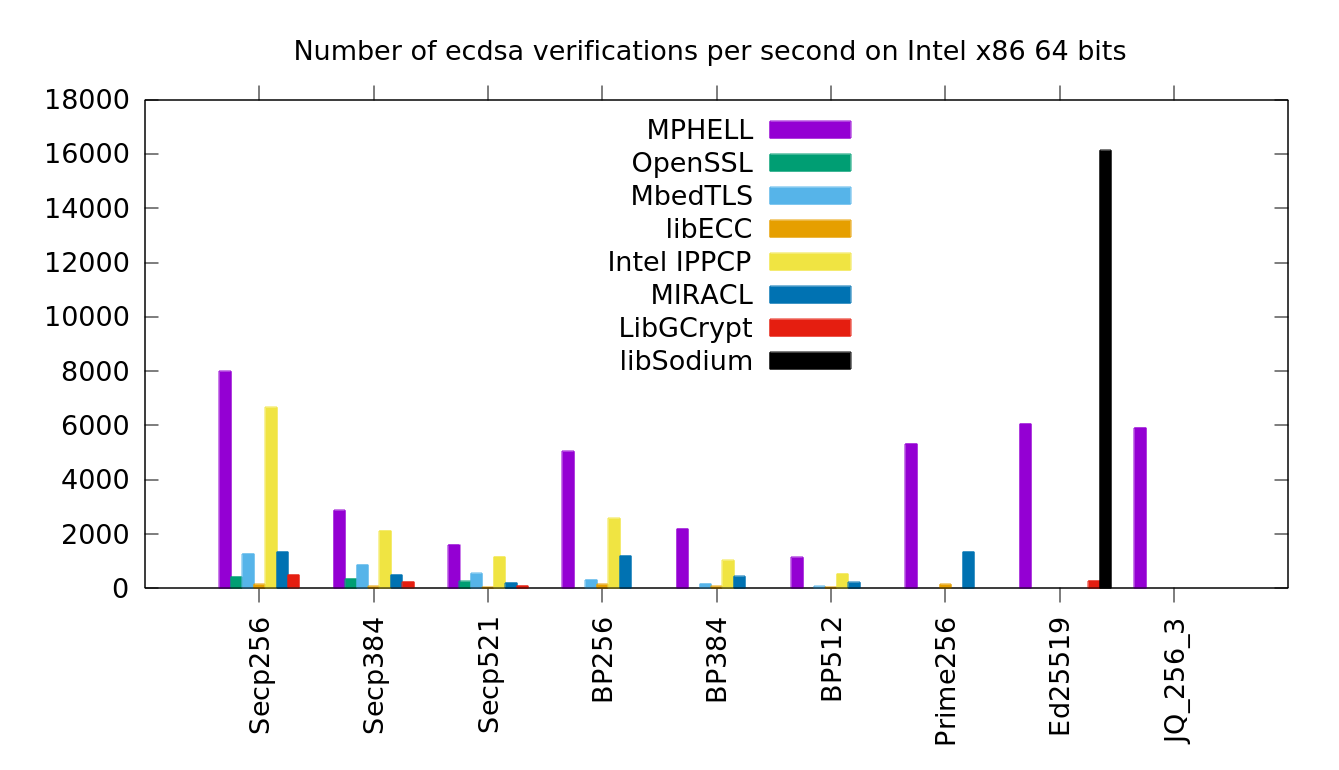
Comparison between MPHELL (using IPP) and other softs for ECDSA verification
Benchmark on STM32F4
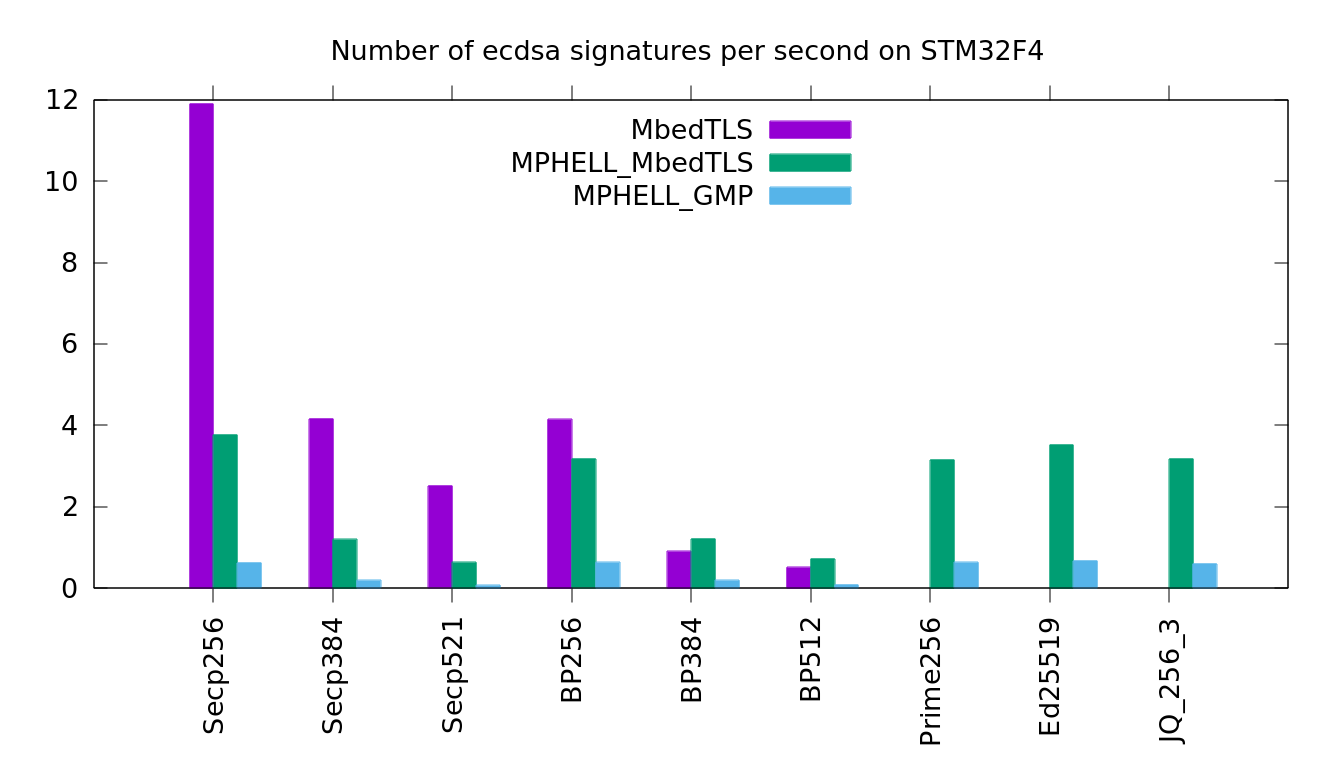
Comparison between MPHELL and MbedTLS for ECDSA signatures
MbedTLS is faster for the signature because MPHELL uses a SPA resistant scalar multiplication (and not a windows one). Moreover MbedTLS has a dedicated arithmetic for the nist curves which is not implemented in MPHELL.
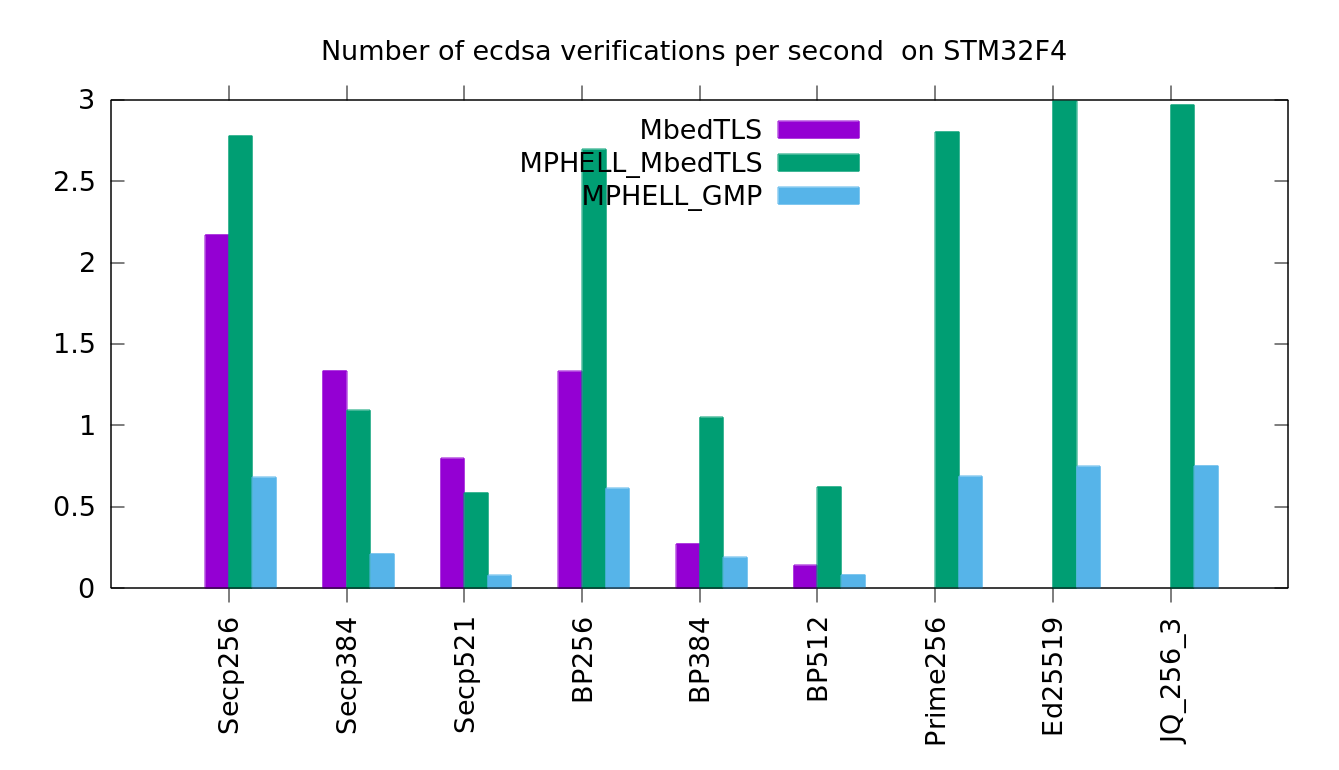
Comparison between MPHELL and MbedTLS for ECDSA verification
MPHELL is faster for the verification because here the security against SPA is not required and we use an efficient sliding windows scalar multiplication.


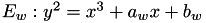
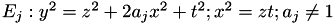
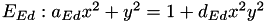
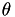 such that
such that 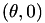 is a 2-torsion point on the Weierstrass elliptic curve.
is a 2-torsion point on the Weierstrass elliptic curve. 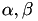 such that
such that 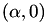 is a 2-torsion point on the Weierstrass elliptic curve and that
is a 2-torsion point on the Weierstrass elliptic curve and that 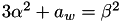 .
. 



 1.8.15
1.8.15